原創 萬物 把科學帶回家

撰文 七君

大家有沒有想過，平時路上的灑水車、鏟雪車，還有馬路清掃是怎么規劃行車路線的呢？

有人會說，這還不簡單，哪兒沒有跑過就去跑一遍不就行了嘛。

這種方法的確能保證所有的道路都被打掃了，但是車子可能會在某幾段馬路上重復開，損失燃油和時間。

北美的一個大城市多倫多在好好用數學規劃之前，每年就白白多花了3百萬美金的冤枉錢。

是這樣的，掃馬路、灑水車、鏟雪車這類問題在數學上屬于中國郵差問題，中國郵差問題本身早在20世紀70年代就有了靠譜的解法。

事情還要從1962年說起。我國數學家管梅谷就想到了這樣一個問題：一個郵差走遍每條街道去送信，最短路徑應該是什么樣的？

后來，美國國家標準技術研究所的數學家 Alan J. Goldman 把這個問題命名為“中國郵差問題”。

到了1973年，加拿大滑鐵盧大學的數學家 Jack Edmonds 和 IBM 研究院的計算機科學家 Ellis L. Johnson 提出了一個至今無人超越的有效算法。他們的算法要 cue 到三百年前的一個人，那就是歐拉。

其實，歐拉在1735年就研究過一個和管梅谷類似的問題——七橋問題，并得到了一些重要的結論。

七橋問題 圖片來源：wikipedia

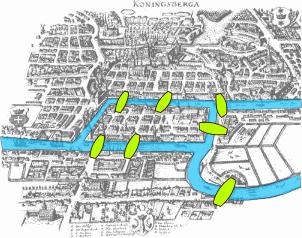
七橋問題和我們小時候玩的一筆畫的益智問題類似：在普魯士的柯尼斯堡有兩個小島，兩個小島和附近一共有7座橋連通。現在問題來了，怎樣規劃路線才能恰好經過每一座橋一次？

第二年，歐拉發了一篇論文，證明七橋問題不可解，原因是他給出了能解的一般條件，那就是每塊地都必須有偶數座橋，而七橋問題不符合這種情況。

后來，這類問題在數學上發展成了圖論和拓撲學。而因為歐拉的開創性貢獻，能夠一筆畫的圖被叫做歐拉圖，一筆畫的路徑被叫做歐拉路徑。

七橋問題等價于右邊這個圖形。歐拉證明，只有當奇頂點的數量等于0或2時，才存在一筆畫。七橋問題的奇頂點（藍點）的數量等于4，因此無法一筆畫。

歐拉還證明了一張圖能一筆畫的一般情況：奇頂點（也就是邊的數量是奇數的頂點）的數量等于0或2。

所以按照歐拉證明的定理，中文的“串”就可以一筆寫成，因為它的奇頂點只有最上面和最下面一共兩個。

串的奇頂點有2個（最上和最下），因此可以一筆畫。

下面這個德國兒童的傳統娛樂項目——Haus vom Nikolaus puzzle （圣尼古拉房屋）也可以一筆畫——

順便說一下，圣尼古拉房屋有44種解法。

把歐拉證明的結論推廣到中國郵差問題的情況，最難搞定的是奇數分叉的道路，遇到三岔路口、五岔路口，走回頭路幾乎是必然。所以 Edmonds 他們的算法是，把奇數路口拎出來單獨算，找到這些路口間的最短路徑；而偶數岔路之間必然存在只走一次的方法，最后把兩部分拼起來就可以了。但是呢，實際生活中掃馬路、灑水和鏟雪要比這復雜得多。

比如，高速公路的整潔對司機的生命財產安全更重要，所以要早點清掃完畢；一些路段是單行線，或者對大型車輛限行。此外，“郵差”也不只一個人，而且不能無限“肝”活，清潔車之間的交接班也要考慮在內。

因此在現實生活中，中國郵差問題很難找到最優策略，這也是為什么一開始 Edmonds 的算法沒有得到廣泛應用。

到了20世紀90年代，隨著計算機技術的進步，一些數學家開始嘗試把中國郵差問題應用到日常生活中。比如，明尼蘇達大學的數學教授 Peh Ng 就曾用圖論的思想幫明州莫里斯市政府規劃冬季的鏟雪線路。

而從2001年開始，北美的一些大城市就開始用比較成熟的軟件（如 ArcGIS）來規劃鏟雪車的行車路徑。這些軟件一般會把一大塊城市交通網分割成一小塊一小塊的，然后分別再進行計算。

比如，多倫多在用圖論原理對鏟雪線路進行規劃后，鏟雪費用比之前減少了三分之一，每年節省了大約3百萬美金（約合2千萬人民幣）。

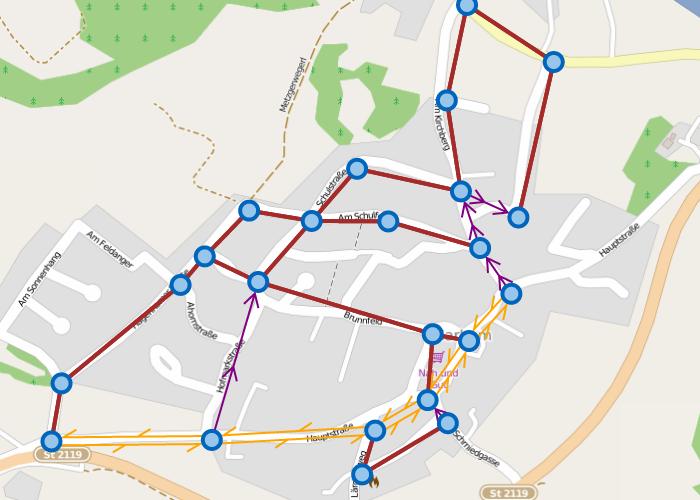
多倫多的市政道路交通的運營經理 Hector Moreno 表示，在用ArcGIS之前，行車路線主要靠經驗和人工計算，現在就不需要這么麻煩了。

波士頓市政府的應用數學團隊 圖片來源：boston.gov

2010年，波士頓市政府也組建了自己的數學團隊——Mayor's Office of New Urban Mechanics，用數學和計算機來規劃鏟雪路線。

像波士頓這樣的大城市用數學進行規劃真的太有必要了。2015年，為了鏟雪，波士頓的鏟雪車一共開了47萬千米，差不多可以繞地球12圈了。鏟雪的花費也是驚人的，那年的暴雪讓波士頓一共掏出了3500萬美金（約合2.3億人民幣）。

2015年，波士頓的暴雪創下了記錄。圖片來源：newyorktimes

除了道路養護，中國郵差問題的算法在很多領域還有應用。比如在交互設計時，中國郵差問題就被用于終端產品的可用性檢測。

舉個例子，一個手機被制造出來以后，手機制造商想要看看每個功能是不是和名稱相符。比如按下主鍵，點開“設置”，再點開“網絡”，是不是真的會出現網絡設定功能。

因為手機的功能很復雜，不同功能之間形成的網絡要怎么樣才能有效地走個遍，這個問題有時連制造商也搞不太明白。1996年諾基亞出的2110的菜單有88個項目，一共有273種操作。如果隨便按，可能一些菜單永遠也不會得到檢測。

但是利用中國郵差問題的算法就能規劃測試路徑和計算步驟數量了：最少就只需要按594次鍵盤按鈕就可以把所有的菜單和功能都過一遍了。

在檢查網頁鏈接有沒有“死角”的時候也可以用到中國郵差問題的算法。

比如，富蘭克林故居的網站(benjaminfranklinhouse.org)有66個網頁，1191個超鏈接。如果網絡測試員沒有頭腦一頓亂點，不但要做無用功，有些網頁和鏈接可能還點不到。但是利用中國郵差問題的算法，測試員知道只要點2248次就可以測試完所有的網頁和超鏈接了。

位于英國倫敦的富蘭克林故居

歐拉路徑判定挺好掌握的呢：口中串串，乃米田共。

把科學帶回家

ID：steamforkids

原創文章版權歸微信公眾號

“把科學帶回家”所有

轉載請聯系 bd@wanwuweb.com

原標題：《用高等數學清掃馬路，這個國際大都市每年省下了2千萬人民幣》

閱讀原文