原創 張江 集智俱樂部

導語

近期新型冠狀病毒（2019-nCov）引發的疫情備受關注，已經有一些針對病毒起源、機理、傳播的研究。春運返崗大潮將至，多地區紛紛限制公共交通，背后的原因是什么？本文特別關注由于人群遷徙引起的病毒傳播和疫情擴散，根據經典論文提出的方法，采用截至 1 月 28 日的最新人流數據，預測人群遷徙背景下，疫情在多個城市二次爆發的風險，并嘗試為多個地區的交通管制提供理論支持。

聲明：本文在無人為干預的假設下，依據《The Hidden Geometry of Complex, Network-Driven Contagion Phenomena》一文提供的方法，針對現有數據進行了初步分析，僅作為科學探討，不構成決策依據。在現有的強力交通管制下，疫情擴散速度應遠小于本文預測的數據。

新型冠狀病毒（2019-nCov）的爆發牽動著全國14億人民，甚至是全球70億人的心。病毒傳播的速度非常之快，我們有必要通過大數據分析，建模模擬等手段對數據進行分析。

目前，無論是正式學術刊物發表的文章還是網絡上傳播的文章來看，大多集中在對于新型冠狀病毒的來源，以及傳播特性的估算。特別是，基本再生數作為一個能夠反映病毒傳播速度的參數引起了廣泛的爭論。然而，目前的這些討論大多集中在對武漢疫情的分析，而較少關注疫情隨著人類的遷徙行為而引發的全國乃至全球城市的傳播。也有一些文章通過各種渠道的人類遷徙數據來分析病毒的傳播，但這些分析大多是對從武漢遷出的各種渠道的流量進行計算，尚沒有討論這些遷徙行為對病毒在其它城市的爆發進行廣泛的討論。進一步，目前我們尚未看到對這種二級爆發現象的定量分析文章。

本文將試圖對由于大量的人口流動而導致的病毒二級甚至三級爆發的可能性進行了探討。而且，我們采用的是定量化計算機模擬與數據擬合并進的手段來完成的多城市間病毒傳播與擴散行為的分析。我們采納了2013年Dirk Brockmann與 Dirk Helbing二人合著的經典文章《The Hidden Geometry of Complex, Network-Driven Contagion Phenomena》一文（后面簡稱《幾何》）中所述及的方法，并結合利用百度遷徙公布的每個城市到各個目標城市的流出比例數據，以及澎湃新聞美數課整理提供數據，以及2016年的百度遷徙數據等多數據來源選定參數進行建模分析的。

一、有效距離

在《幾何》一文中，作者們提出了一種全新的距離概念，被稱為有效距離，并聲稱在病毒擴散傳播中，該距離遠比地理距離起到了更加至關重要的作用。那么，這種有效距離是什么呢？其實就是現代人類乘坐交通工具進行的長程遷徙而形成的一種幾何效應。

具體來講，我們不妨假設人們是一個毫無目的的隨機游走粒子，則它們的一些可能從A出發沿著交通路網中的所有可能路徑到達B地，在這些粒子中，最先到達B的粒子所跳轉的步數就是有效距離。這種情況下，即使A和B沒有道路，粒子也可能通過其它城市中轉到B。另外，就是當粒子從A出發有多個城市可以到達的時候，它會按照交通流量大小而隨機選擇下一步的城市。總之，有效路徑可以更好地刻畫人們乘坐交通工具的出行行為。

我們將最新2020年的從百度遷徙上獲得的流量比例數據混合2016年的流量數據得到任意兩城之間的跳轉概率，并根據這個概率計算得到任意兩城市之間的有效距離。我們可以看看，從武漢出發到達的所有城市，按照有效距離從小到大的順序排序得到：

圖 1. 有效距離從小到大的順序排序

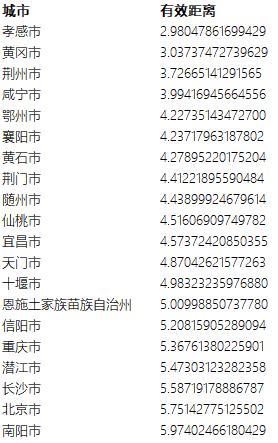
那么，根據《幾何》中的結論，這個排名基本就是病毒傳播在時間上的先后順序了。然而，在大家關注武漢疫情的早期，無論是媒體還是公眾都忽略了諸如孝感、黃岡、荊州等湖北省的非武漢城市。而最近的疫情爆出了這幾個城市的感染人數都是非常大的，這從另一個角度佐證了這個有效距離的有效性。

在之前的一些文章中，有人根據武漢出發的交通流量數據來估算最容易被感染的城市，這是有道理的，事實上在我們的數據中，有效距離與流量之間有著非常好的負相關性：

圖 2. 有效距離與流量之間的相關性

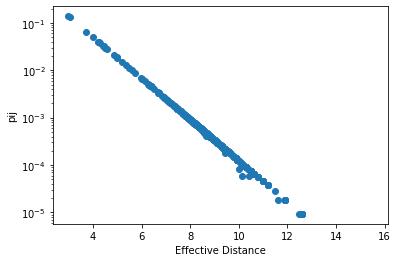
該圖即佐證了有效距離與流量之間的關系。可以說從武漢出發到達某城市的流量越大，則該城市爆發疫情的時間就越早。

實證數據是否支持我們的判斷呢？讓我們將疫情數據代入進來，并計算得到每個城市最先報道病例的時間，然后去看這一時間與該城市有效距離的關系，如下圖：

首先，我們來看有效距離，該數值可以衡量病毒擴散到該城市的快慢和先后順序。我們繪制出首報病例的發病日期和有效距離的關系：

圖 3. 首報病例的發病日期和有效距離的關系

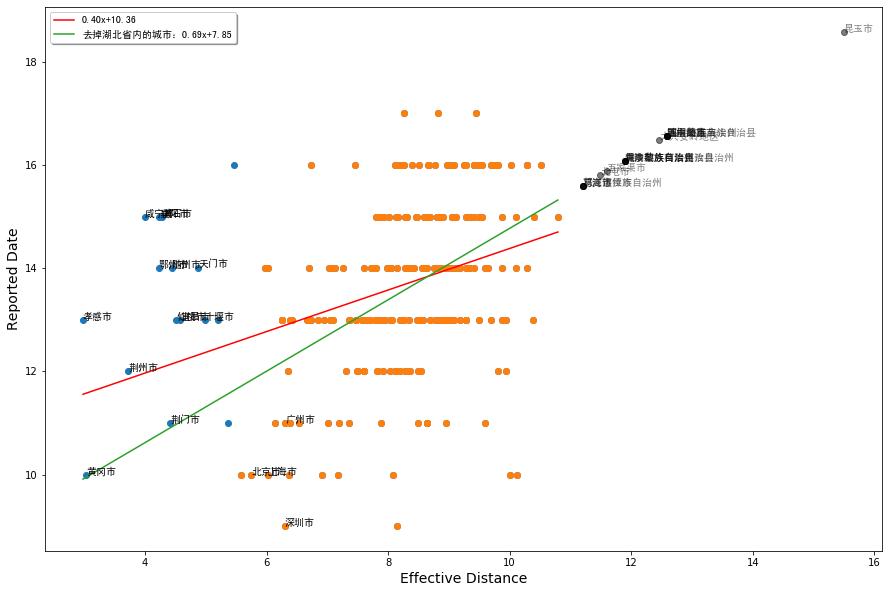
我們采取了兩種擬合方式，一種是忽略湖北省的大部分城市，因為我們懷疑這些城市報告的病例并不準，很有可能病毒比報告日期更早地到達了這些區域（見下文討論），則可以得到更高的斜率，決定系數RSquare也會從0.34提高到0.43。

但是，這種相關性并不強，遠比《幾何》文章里匯報的結果要差。分析原因有可能有三個：一是《幾何》一文大多匯報的是全球尺度、國家級別的傳播事件，利用航空數據做估算會比較準確。而我們的流量數據可能不夠準確，在基本假設上也可能不滿足該文的要求。二是可能縱坐標的這種病例確診時間遠比疾病的首達時間要晚很多。而且，對于部分湖北省內城市，這一偏離可能會非常大。

為了驗證這一猜測，我們可以用 “nCoV疫情地圖”項目組提供的包含了病人自己匯報的感染日期來計算的首報病例時間來進行作證。

圖 4. 病人自己匯報的感染日期來計算的首報病例時間

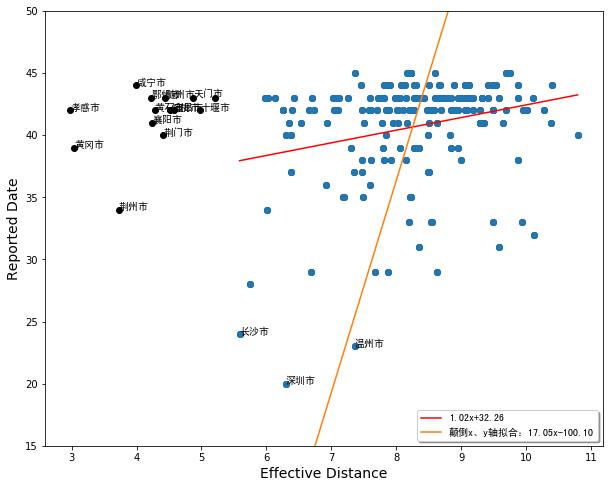
該圖中，橫坐標同樣是有效距離，縱坐標則是清華數據中病例匯報的感染時間（如果這一數據缺失，則我們仍然用確診時間補充）。在該圖中，我們能明顯看出長沙、深圳、溫州等市匯報的日期要比一般城市的匯報日期更短。因此，我們懷疑，湖北的城市有明顯遲報的現象。因此，我們在做第二條擬合線的時候，忽略了這些城市。特別是對于圖4，忽略之后的擬合線的斜率達到了17左右，這個數量級是與《幾何》一文中一致的。

除了驗證這一關系外，我們還可以得到一些預測結果。如圖3中，右側部分延展出去的城市都是一些目前尚無報告病例，而我們根據外推估算出來的首發病例報告時間，例如北屯市將在1月25日左右發現，而昆玉市將可能在29號左右發現。

二、病毒爆發趨勢

《幾何》一文還給出了一個交通網絡上的病毒擴散傳播模型，該模型是在SIR模型的基礎上改進而得到的，其方程如下：

(1)

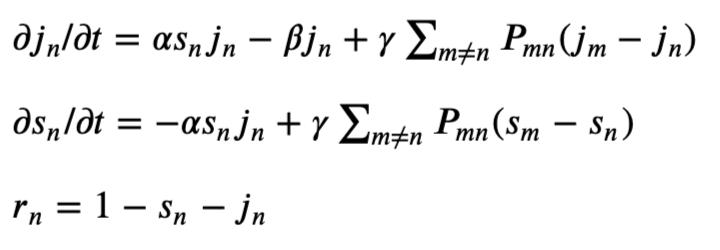
其中jn是n城市感染比例；Sn是n城市疑似人群比例，rn 是n城市恢復健康或死亡的人群比例。α，β，γ 都是參數。下面，分別進行解釋并給出取值說明。

所有這些參數的取值均根據實際數據得到(R0 世界衛生組織給出的數據是2.3左右，普遍估計是3.5以下，而我們采納了比較高的3.8是基于如下原因：如果我們認為治愈率的估計0.1是合理的，那么根據SIR模型，只有當R0取3.8才能較好地吻合實際數據的情況）。那么，這個模型和這組參數和各個城市實際的確診病例的觀測情況符合得怎么樣呢？我們可以看下圖：

圖 5. 模型和這組參數與各個城市實際的確診病例的觀測情況符合程度

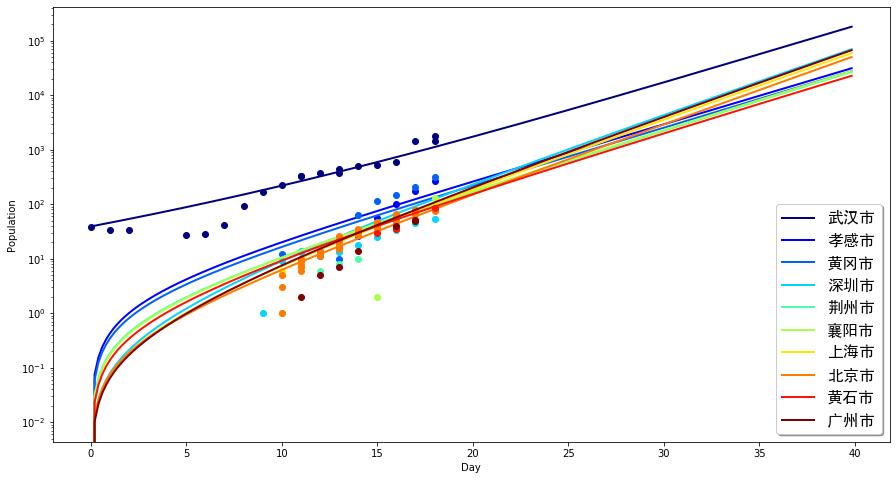
該圖橫坐標為從1月10日（我們數據中的第一個確診病例日期）開始的時間，單位是天。縱坐標是不同城市中感染人口。我們挑選了一些武漢周邊的城市和北京、上海、廣州、深圳這樣的大城市，將實際數據與模型計算的結果進行了比較（由于實際情況是指數增長，故而，我們將縱坐標軸取了對數）。我們發現，模型與數據吻合得非常好。這說明我們的模型是可用的。

接下來，就讓我們看看，當保持這組參數不變，也就意味著如果我們不采取任何措施的情況下，病毒擴散的情況：

圖 6. 如果我們不采取任何措施，病毒擴散的情況

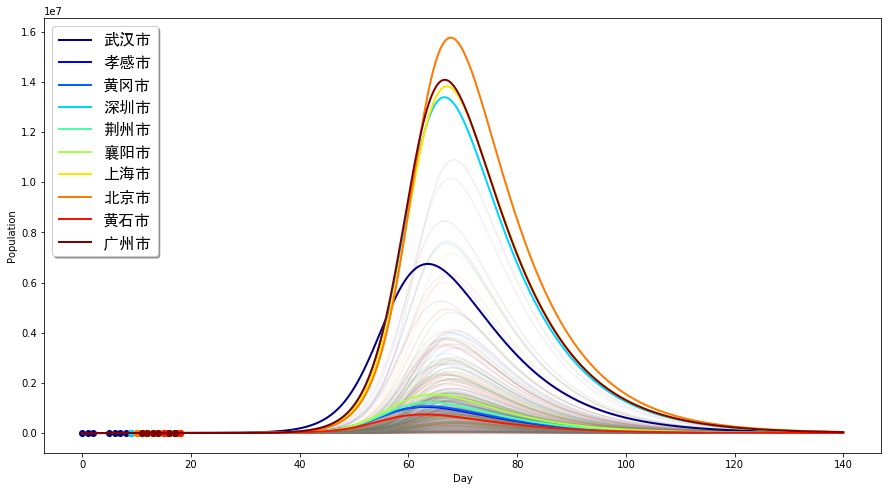
該圖就是病毒在無任何限定條件下的擴散傳播情況，幾個選出來的觀察城市用不同顏色較清晰地繪制而出，而所有城市用了比較淡的顏色作為背景繪制而出形成一個帶形區域。另外，目前我們能夠得到的數據也繪制在了同一張圖上，用圓圈點表示（左下角）。從這張圖中，我們能夠得出以下一些結論：

在不采取任何措施的情況下，現在疾病的擴散仍然處于非常早期的階段（左下角）；而真正的指數增長大爆發要到大概距今20天左右的時間才到來。

在自然條件下，疾病最終退去要等到距今大概120天以后，也就是5月底將近6月。

感染人口最多的城市將是北京，而非武漢，這是因為北京人口基數更大；而其他幾個大型城市的感染人數都會比武漢多。縱坐標的數字是10的7次方數量級，這意味著，如果我們不控制疫情的話，感染人數將達到千萬量級。比如北京峰值會接近1千6百萬。

對于我們關注的城市來看，疾病擴散會明顯存在著兩個峰，第一個峰是以武漢為首的湖北境內城市，將會在45天后左右到達高峰；第二個峰則是以北京、深圳等大城市為主的，這個峰得到來會比武漢推遲將近10天左右。因此，大致可以說，北京、廣州等大城市在“拷貝”十天前的武漢的發展情況。

這表明我們的管控措施絕對是必要的，我們要積極配合。

三、疾病的干預與控制

這些結論可能有些過于駭人聽聞，毛骨悚然了。但別忘了，這是在絕對自然的情況下。而現實情況是，我們早已經全社會動員起來了，我們已經對疾病的傳播進行了干預和控制。那么，如果將這種干預控制引入到我們的模型中會帶來什么效果呢？接下來，就讓我們來建模這種情況。

首先，我們將介紹我們的建模思路。在基于（1）式的基礎上，我們引入了一個 ξ 項，如下式：

(2)

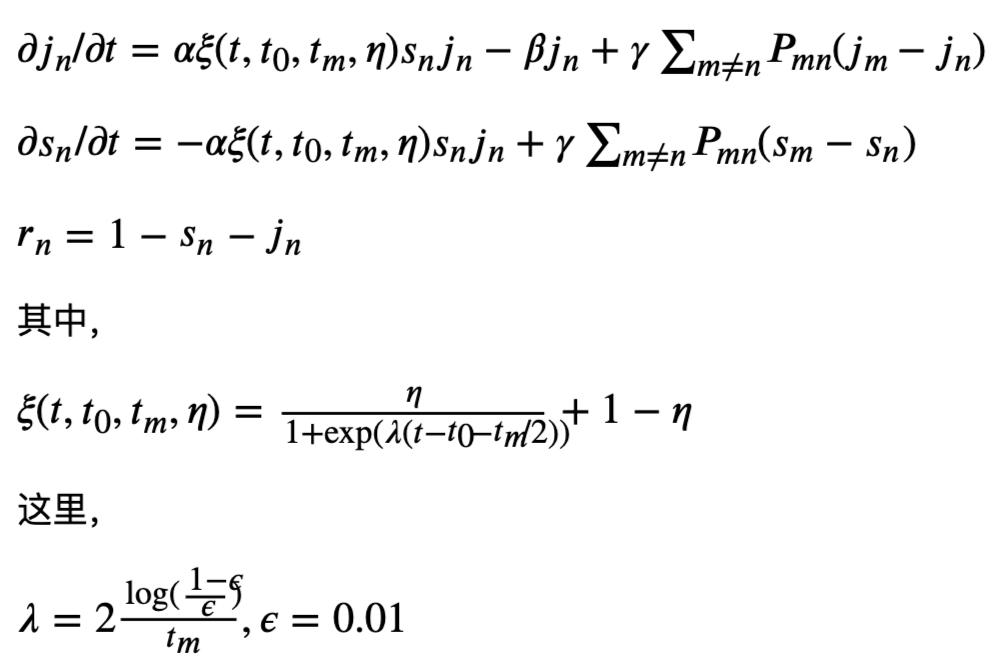
這個 ξ 項就模擬了我們人為干預、控制疾病傳播的因素。首先， ξ 是一個介于 η 到1之間的小數乘到了（1）式中的交互作用項上面了，和 α 起到了等同的作用，直接影響健康者與感染者的交互概率。其中 η 是我們人為控制能達到的最小值，這個可以根據能夠達到的最小的基礎再生數估算出來（后面詳細給出）。這個 ξ 是 t 的函數，并且由一組參數：t0, tm 和 η 來控制，也就是說 ξ 會隨著時間 t 而變化。

為了形象化看到 ξ 的作用，我們還是繪制出了圖形：

這是一條隨t而逐漸從1衰減，以至于降低到最小值為 η =0.2的數值，表示了我們對疾病的控制作用的強度情況， ξ 越大，控制力度越小，反之越強。

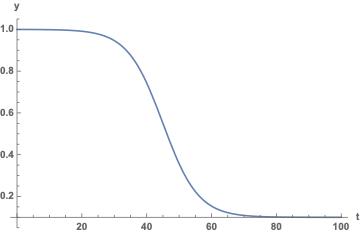
我們觀察這個曲線，有兩個關鍵拐點，一個是開始顯著下降的點，這個點由參數t0來刻畫，表示我們全國開始對疾病進行了干預控制，上圖曲線，t0=20；第二個拐點是曲線顯著接近于0.1的時間（從t0開始計時），這個時間長度就是我們最終完全將疾病控制住所需要花費的時間，用參數tm來刻畫。在上面的曲線中，tm=50。

那么，這些參數怎么取值呢？見下表：

首先，按照最樂觀的估計，我們假設全社會動員以后，人們平均交互的數量減少為原來的1/4，這樣就可以讓基本再生數降低到原來的1/4，即0.95左右，我們需要20天左右讓全國達到這樣的水平，則疫情發展的曲線如下：

圖 7. 假設全社會動員以后，人們平均交互的數量減少為原來的1/4，疫情發展的曲線

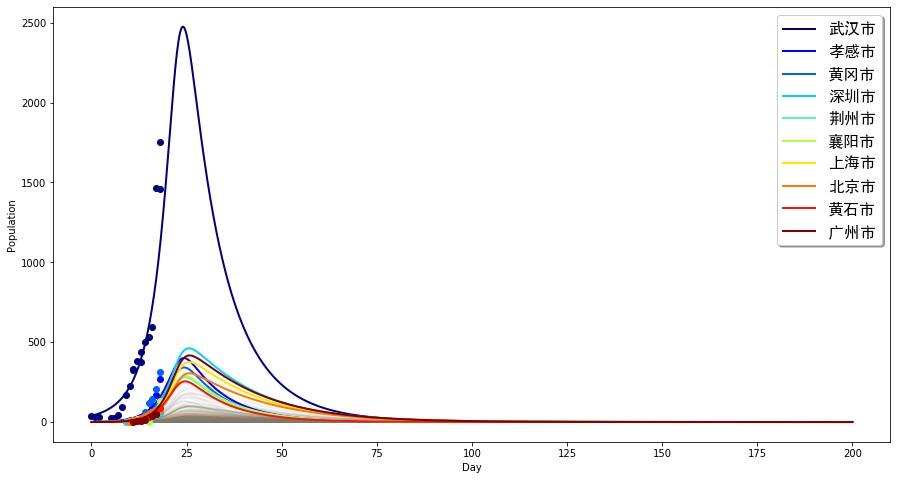
橫坐標為時間（1月10日為原點），縱坐標為每個城市感染人口的數量。在這種情況下，我們可以看到，各個城市基本都將會在一周內達到峰值。且武漢感染最多可達2500人左右就開始回落，而深圳市將會達到500左右，其它城市均不到500。而最終感染完全消失要到差不多距今80天以后。

那么，如果更合理一些，我們的管控措施并不能很快地將全國人民動員起來，可能要等到一個月以后才達到目標效果（基本再生數降低到原來的1/4），那么，得到的模擬曲線是：

圖 8. 管控措施在一個月以后才達到目標效果時得到的模擬曲線

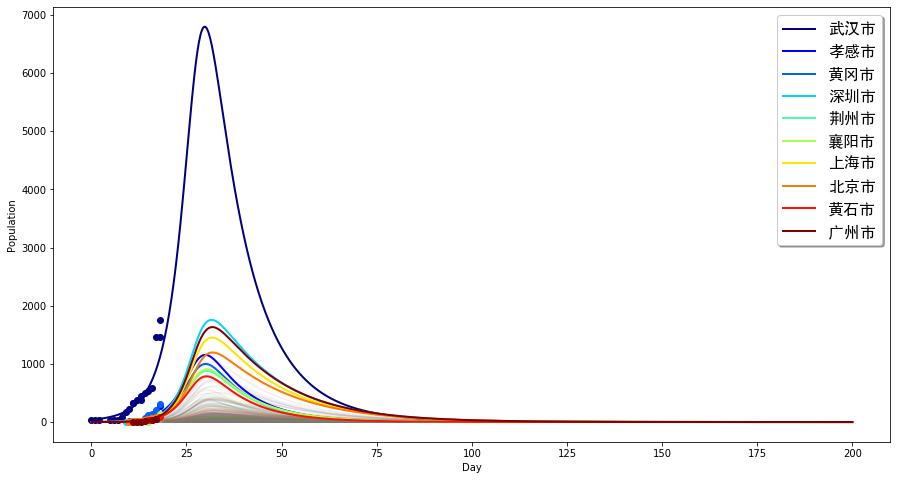
與前面的曲線比，形狀沒有發生很大變化，但是峰值會明顯延后和提高。大概將在距今10天后達到（這一數字和鐘南山最新的估計是差不多的），最高到達接近7000的人數，深圳、廣州等差不多落后3-5天達到峰值，差不多2000。然而該疾病再過了峰值以后仍然會維持相當長時間的時間，該疾病擴散將維持到80天以后，即到4月份。

其實，這一情況也有可能出現。雖然我們生活在大城市的人都接觸這方面消息非常多，因此比較謹慎，管控效果很好。但是，考慮到絕大多數偏遠地區、小城鎮，則人們可能普遍意識不夠強；抑或者過幾天的春運高峰的到來也有可能會增加人們交互的比例，而出現這種情況。

下面讓我們考慮最糟糕的一種情況。假設我們需要100天（3個月多）的時間，將疾病基礎復制數控制在原來的1/4，則會出現下面的情況：

圖 9. 假設最糟糕的情況需要100天將疾病基礎復制數控制在原來的1/4，則得到模擬曲線

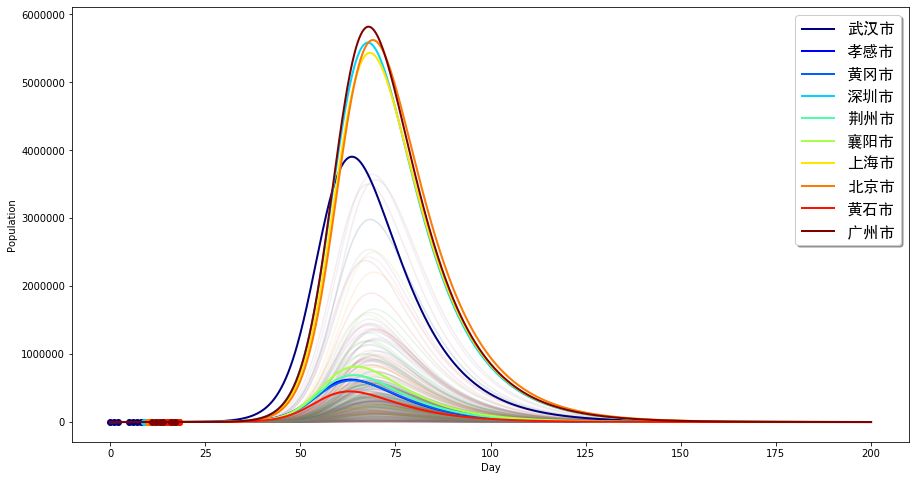
這其實與沒有控制的情況差不多。疾病將在大概50天后達到峰值，而且廣州、深圳的峰值會遠比前面的情況高，武漢、廣州等城市最高可達600萬不到的感染人數。

在第一種比較保守的估計情況下（即在30天內將病情控制住），我們可以計算全國總的感染人數和死亡人數。我們用病死率來估算死亡人數，考慮到隨著人們治療該病的手段及其疫苗的研制會逐步提升，我們假設最終該病平均的致死率按照3.1%來計算，那么可以得到全國相應的累積死亡人數曲線。我們將全國總感染人數、累積康復人數和累積死亡人數繪制成如下圖：

圖 10. 全國總感染人數、累積康復人數和累積死亡人數

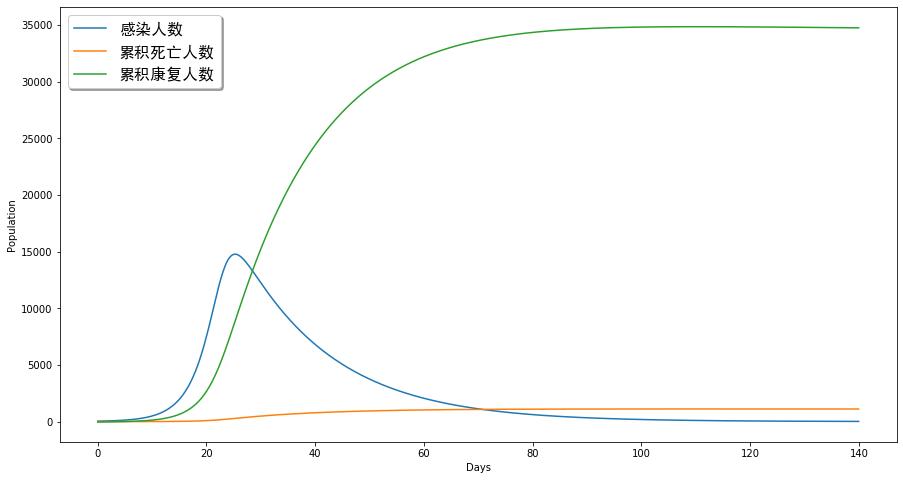
即累積感染人數總量將達到3萬5千人，死亡人數將接近1200人。這個數字看起來可能偏向保守，但是如果我們考慮如下因素也有可能正確：

大量確診病例很有可能會被最終治愈，但目前仍然在醫院中觀察，故而可能我們估算的死亡比例會過高了；

隨著我們對病毒的認識，以及疫苗的研發，將會使得死亡率大大降低，從而導致我們的這個數字估計過高。

死亡人數將接近1200左右。

總之，nCov雖然來勢兇猛，但是如果我們加強管控力度，該病毒還是有可能得到有效控制的。我們期待著這場戰爭最終的勝利。

參考文獻：

[1]D. Brockman and D. Helbing: The Hidden Geometry of Complex, Network-Driven Contagion Phenomena, Science 2013

[2] J. M. Read, J. R. E. Bridgen, D. A. T. Cummings, A. Ho, C. P. Jewell, Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions, Preprint in MedRXiv 2020.

[3] 周濤文章:

https://new.qq.com/omn/20200126/20200126A08P9W00.html?pc

數據來源：

1、疫情數據由澎湃新聞美數課整理提供 ，并參考“nCoV疫情地圖“項目組整理的疫情數據

2、2016年百度遷徙數據

3、2020年百度遷徙部分比例數據

項目地址：

在此我們公開本研究的GitHub項目，歡迎大家找到我們的錯誤，并批評、挑戰這個模型，項目地址為：

https://github.com/jakezj/hidden_geometry_of_nCoV

我們的數據來源有限，如果大家有更精確、更詳細的相關數據，請聯系相關負責人微信：18621066378

附錄：

有關有效路徑的進一步解釋：

具體來說，如下圖，假設從A到B及其周圍城市的交通路徑（可包括飛機、火車、汽車等一切手段）如左圖所示，而其流量大小如連邊上的數字所示。當我們計算有效距離的時候，我們先要將連邊上的流量數字轉化為占比數字，即從A到B的流量所占從A出發的所有流量的比例，如右圖所示。

附錄 1. 有效數字的賦值解釋

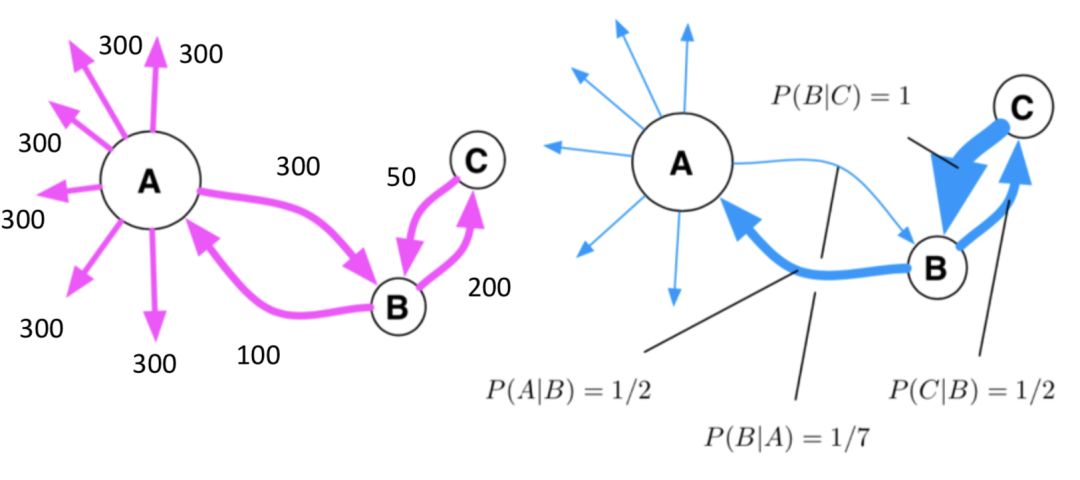
這個時候，我們就能計算有效距離了。例如，A到B的有效距離就是

d(A-->B) = 1 - logP(B|A)=1-log7

為什么要取對數，為什么又要減1？這個請聽我在線上講座的解釋（講座視頻錄像見文末）：為什么病毒擴散這么快？從網絡科學視角看大規模流行病傳播。

然后A到C的有效距離可以這樣來算：

也就是對于間接相連的兩個點，我們只要求出中間路徑的有效距離，再把它們加到一起就可以了。

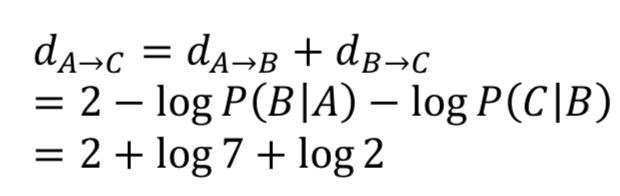
當兩點之間存在著多條路徑的情況下，我們可以遍歷所有路徑，并用有效距離最短的一條作為最終的兩點間的路徑長度，如下面的從A到D的例子：

附錄 3. 多條有效路徑中最終有效路徑的確定

致謝：

感謝董磊、章彥博、網友烏克里協助數據建模分析，感謝“澎湃新聞美數課”、“nCoV疫情地圖“項目組、百度遷徙、丁香園的數據源。

作者：張江

審校：劉培源

編輯：趙千里

推薦視頻

2013年Dirk Brockman等人在Science上發表的The Hidden Geometry of Complex, Network-Driven Contagion Phenomena一文就指出疾病的傳播其實與城市間的地理距離沒啥關系，而與城市間的“等效”距離密切相關。這里的等效距離就是指根據城市間交通流量數據而折合以后的距離。北京師范大學張江老師錄制了視頻解讀這篇論文，供感興趣的讀者參考。

課程鏈接：https://campus.swarma.org/play/play?id=11116

我們也在針對武漢到全國各大城市之間的流量數據做分析，歡迎感興趣的朋友參與，詳情請見推文《新型冠狀病毒通過交通流的傳播數據推演（含公開數據集）》。

原標題：《防控力度多大才能遏制疫情發展？ 網絡動力學推演給你答案》

閱讀原文