主題樂園的年卡（或會員卡，以下統稱年卡）是游客購買的，在特定周期內（一般為1年）供游客本人無限次入園的憑證。年卡是主題樂園門票價格體系的重要組成部分，但是，年卡價格應該如何確定，價格高一些好還是低一些好，一直是困擾很多主題樂園行業從業人員的問題。對于年卡價格高低制定的依據有很多，比如為了平衡主題樂園的淡旺季游客量、為了構建主題樂園與游客之間的更加緊密的會員關系、為了向游客提供更好的會員服務提升樂園自身的吸引力等等。本文主要從主題樂園收入最大化的角度，通過定量分析的方式，來探討主題樂園年卡的定價方法，以供大家參考和討論。

▲

主編 | 楊明

責編 | 井翔遠

作者 | 中國游樂特約作者 楊劍川

前提和假設

本文主要通過定量分析的方法來研究問題，有必要提出研究的基本前提和假設，不同的主題樂園可以依據自身的實際情況對相關的參數和前提進行調整，滿足實際分析的需要。

1、關于基本參數的假定

我們假設主題樂園樣本A，它的標準門票價格既定，為P票；每年到主題樂園A游玩的游客人數既定，為N人（注意是游客人數，不是人次數或入園量）；主題樂園A在沒有執行年卡政策（不賣年卡）的情況下，經統計得出的一年重游率為α，備注：重游率=年入園總人次/游客人數（N人）-1；在有年卡政策情況下，經統計得出的周期內年卡游客平均入園天數為F；主題樂園A非年卡用戶園內二消占標準門票價格的比例為β1；主題樂園A年卡用戶園內二消占標準門票價格的比例為β2。

假設以上參數均為統計常量或既定常量，只和一個主題樂園本身的產品特性和所處的環境相關，在分析過程中不隨著自變量和因變量的變化而改變。

2、關于變量的假定

我們研究的核心是年卡價格高低的變動對于總收入的影響，首先研究關于年卡價格變動如何影響購買年卡的游客的比例問題，假定：

自變量x為標準門票價格占年卡價格的比例，即：

x=標準門票價格/年卡門票價格，自變量的取值區間為（0，1）

因變量f(x)為購買年卡的游客占總游客數量的比例，即

f(x)=年卡游客數量/游客人數，因變量的取值區間為（0，1）

3、關于變量的說明

在實踐中我們可以明顯感覺到，自變量x和因變量f(x)有著很強的正向相關關系，當自變量x取值靠近0，意味著年卡價格相對于門票價格來說非常貴，這時候將會導致購買年卡的客群大幅減少；而當自變量x取值越來越靠近1，意味著年卡價格相對于門票價格來說變得比較便宜，這時候購買年卡的游客將會不斷增多。而x和f(x)的取值都不能小于0，因為價格沒有負數，也不能大于1，因為現實中年卡價格不可能低于門票價格。

模型的建立

1、通過回歸分析找到x與f(x)的擬合函數

關于x與f(x)之間的擬合函數，我們首先可以做一個思想實驗：當年卡的價格非常高，高到游客購買一張年卡的價格可以覆蓋全年每天都來主題樂園游玩的散票價格，這時幾乎任何一位游客都不會選擇購買年卡，這意味著x取值趨近于0，f(x)也趨近于0；而隨著x值的增大，f(x)的值將會隨之增大，但是一開始，f(x)增大的速度不會很快，因為年卡還是太貴了嘛；而當x的增大超過一定區間之后，f(x)隨之增大的速度將會快速的增加，因為越來越多的游客開始覺得購買年卡是劃算的，而當x的增大開始接近1的時候，f(x)的增加的速度將會變得非常快，因為只需要在門票的基礎上在加少量的錢就可以購買年卡了，而當x趨近于1的時候，幾乎所有的游客都會購買年卡，所以f(x)也趨近于1，因為年卡的價格和門票價格一致了嘛。這種因變量隨著自變量的增加，一開始增加速度比較緩慢，而后來增加速度大幅提升的關系，非常符合冪函數的關系，所以，在后邊的回歸分析中，我們應該主要選擇冪函數進行擬合分析。

接下來，我們需要找到歷史統計的自變量與應變量的對應數據，以主題樂園A為例，歷史統計數據為：

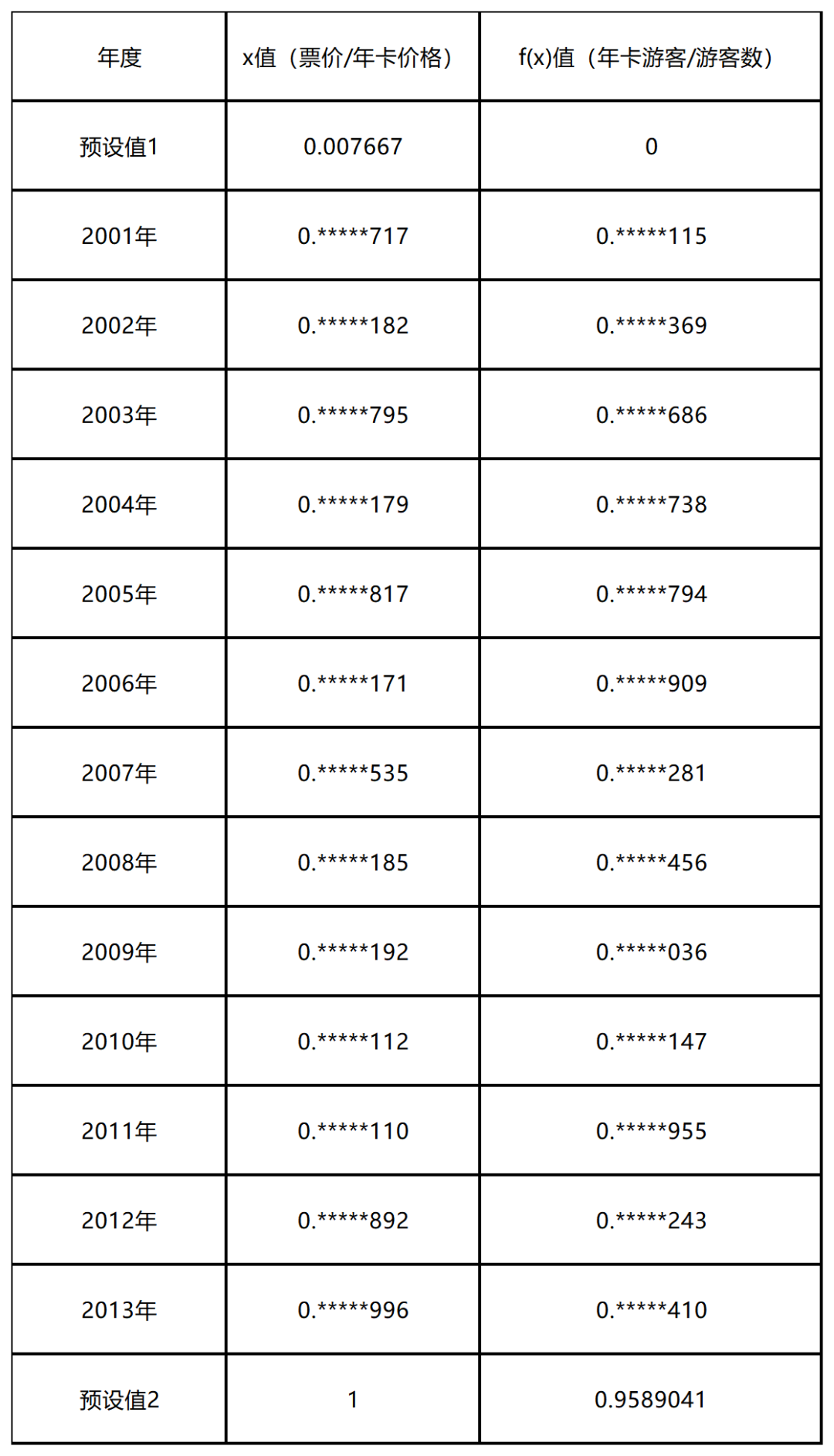
表1：主題樂園A歷史價格比和年卡占比統計表

其中，樣本數據的變化率越大越好，而預設值是按照我們上文的分析和假定，模擬當x取值趨近于0和1的時候的情況。有了樣本數據，我們可以使用統計軟件對自變量和因變量進行擬合分析，按照上邊的分析我們選取冪函數進行擬合分析，如下圖：

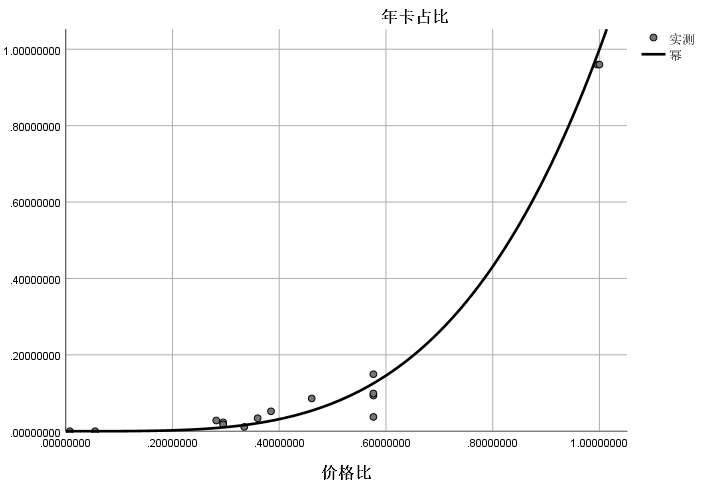
圖1：擬合曲線

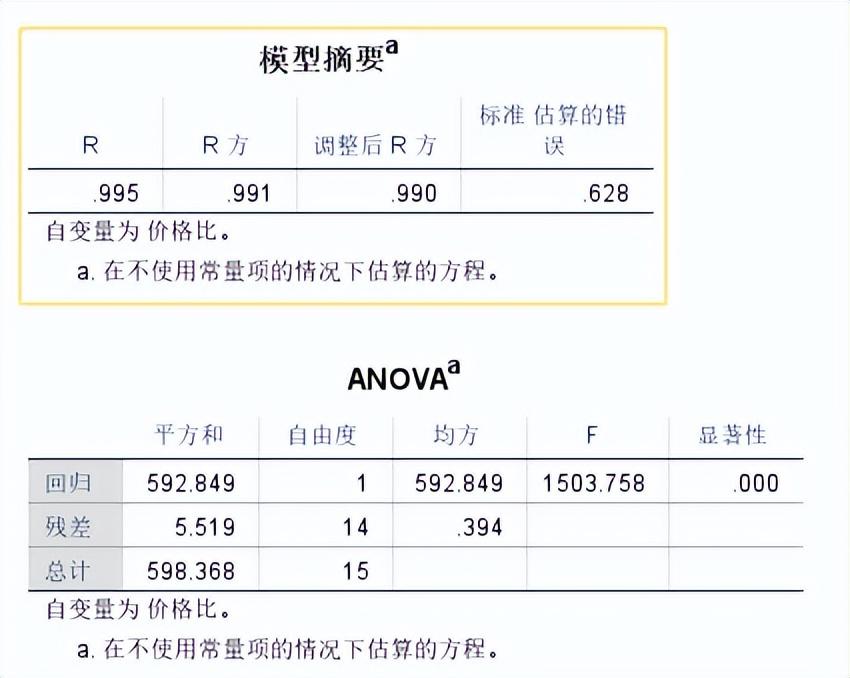
圖2：擬合結果模型摘要

從擬合曲線和模型摘要來看，采用冪函數進行擬合的結果比較吻合，預測程度也很高，因此，通過統計軟件，我們能夠得出擬合方程（文中僅保留2位小數點，下同）：

f(x)= 1 * x^3.77，0＜x＜1

2、建立收入S與價格比x的回歸函數

有了門票價格與年卡價格比x和年卡數量與游客數量比f(x)之間的函數關系，更進一步我們建立收入S和x之間的函數關系。

收入S由兩個部分構成，一個部分是門票收入S1（一消收入），包括周期內銷售非年卡游客門票和年卡；第二個部分是二消收入S2，包括年卡游客和非年卡游客入園后購買餐飲、商品和服務的收入，即：

S=S1+S2

而

S1=非年卡游客總購票收入+年卡銷售收入

S1=P票*（N人-N年）+ P票*（N人-N年）*重游率α*（1-N年/N人）+N年*P年

將f(x)和x代入

S1=P票*N人*（（1- f(x)）+α*（1- f(x)）^2）+ f(x)/x））

其中：“P票”為標準票價，“P年”為年卡價格，“N人”為游客人數，“N年”為年卡人數，α為沒有執行年卡政策情況下的一年重游率

而

S2=非年卡游客二消收入+年卡游客二消收入

S2=（N人-N年）* P票*β1+（N人-N年）* P票*β1*重游率α*（1-N年/N人）+N年*年卡入園頻次F* P票*β2

同樣，將f(x)和x代入

S2=β1*P票*N人*（(1-f(x)）+α*P票*N人*（1-f(x)）^2)+P票*N人*f(x)*F*β2

其中：F為周期內年卡游客平均入園天數；β1為非年卡用戶園內二消占標準門票價格的比例；β2為年卡用戶園內二消占標準門票價格的比例

所以：S1+S2合并后

S=N人*P票*（（1+β1）*（（1- f(x)）+α*（1- f(x)）^2）+f(x)*F*β2+f(x)/x）

模型的分析

1、找到對應最大收入的年卡定價

有了關于S和f(x)、x對應的函數關系，我們就可以通過求x在0-1這個區間上對應的S的極值點，來確定收入最大化的票價和年卡價格的比例了。

根據：

S=N人*P票*（（1+β1）*（（1- f(x)）+α*（1- f(x)）^2）+f(x)*F*β2+f(x)/x）

要求x在0-1這個區間上對應的S的極值點，因為N人、P票都是常數，所以其實就是要求（1+β1）*（（1- f(x)）+α*（1- f(x)）^2））+f(x)*F*β2+f(x)/x在（0,1）的極值點。

我們根據擬合函數

f(x)= 1 * x^3.77，0＜x＜1

將其代入（1+β1）*（（1- f(x)）+α*（1- f(x)）^2）+f(x)*F*β2+f(x)/x，并假定主題樂園A樣本的α=30%，F=6，β1=20%，β2=5%

我們可以得到一個新的擬合函數

F(x)= 1.57-1.64*x^3.77+0.36*x^7.54+x^2.77, ，0＜x＜1

要求收入最大化的極值點，我們只需要對F(x)上求導，并令求導后的方程等于0，即：

F’(x)=0，0＜x＜1

通過觀察函數圖像的單調性所對應的極值點，我們就可以找到對應收入最大化的極值點

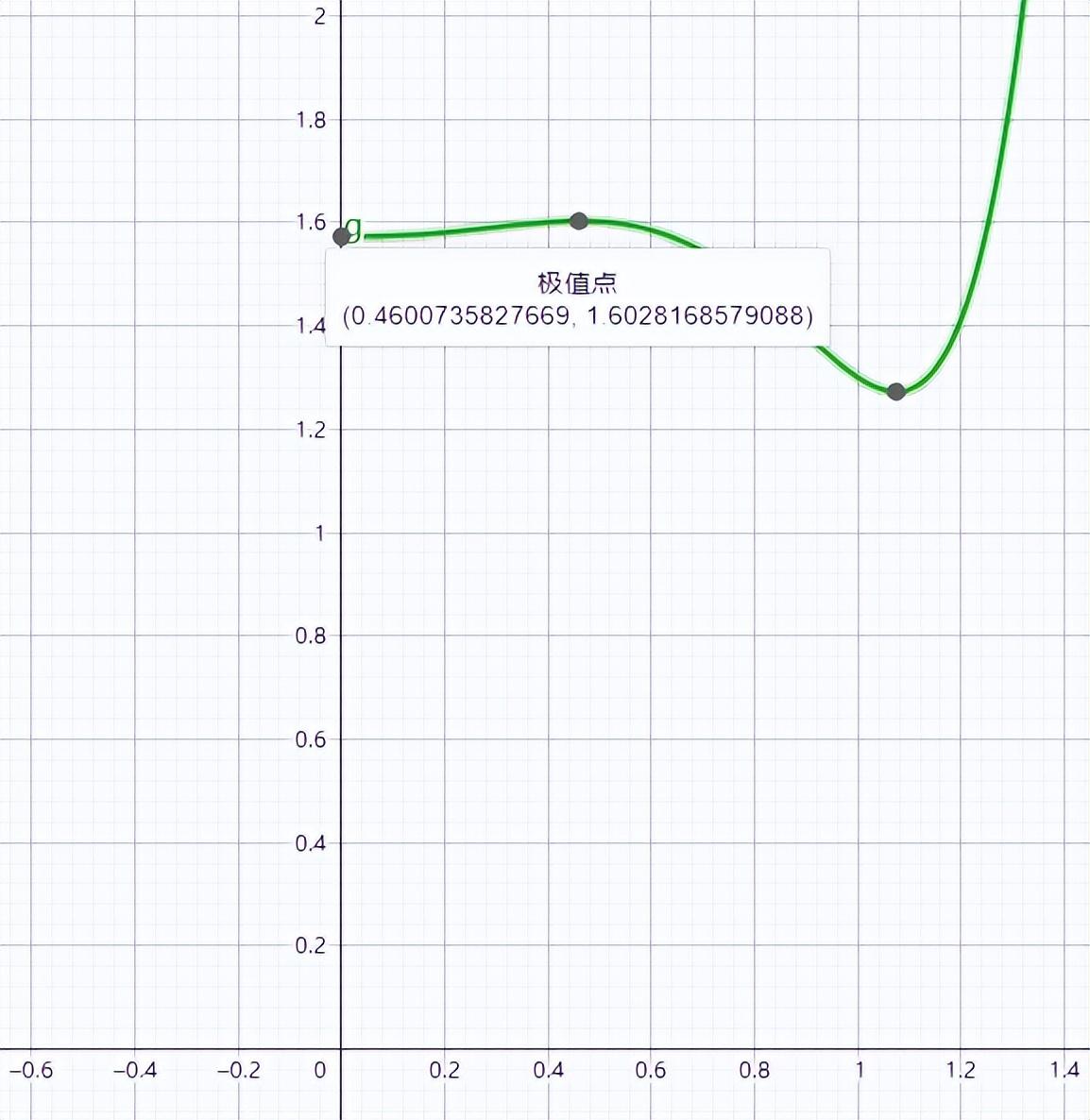
圖3：F(x)函數圖像和所對應的極值點

這表明，按照我們上述假設和參數建立的模型，主題樂園A收入最大化所對應的x值為0.46，即門票價格占年卡價格比例為46%，而在這個價格下，公園總收入達到最大化，系數為1.6。如果主題樂園A的門票價格為300元，那么年卡的價格應該為300/0.46=652元。

2、不同參數對于極值點的影響

在模型中，決定擬合函數的參數有重游率α、非年卡客群人均二消參數β1、年卡人均消費β2和使用頻次F。這些參數的大小，是由一個主題樂園本身的產品和吸引力，客群特點所決定的。現在，我們探討一下這些參數的不同取值對于擬合函數，特別是對于極值點的影響。

（1）重游率高低對于擬合函數的影響

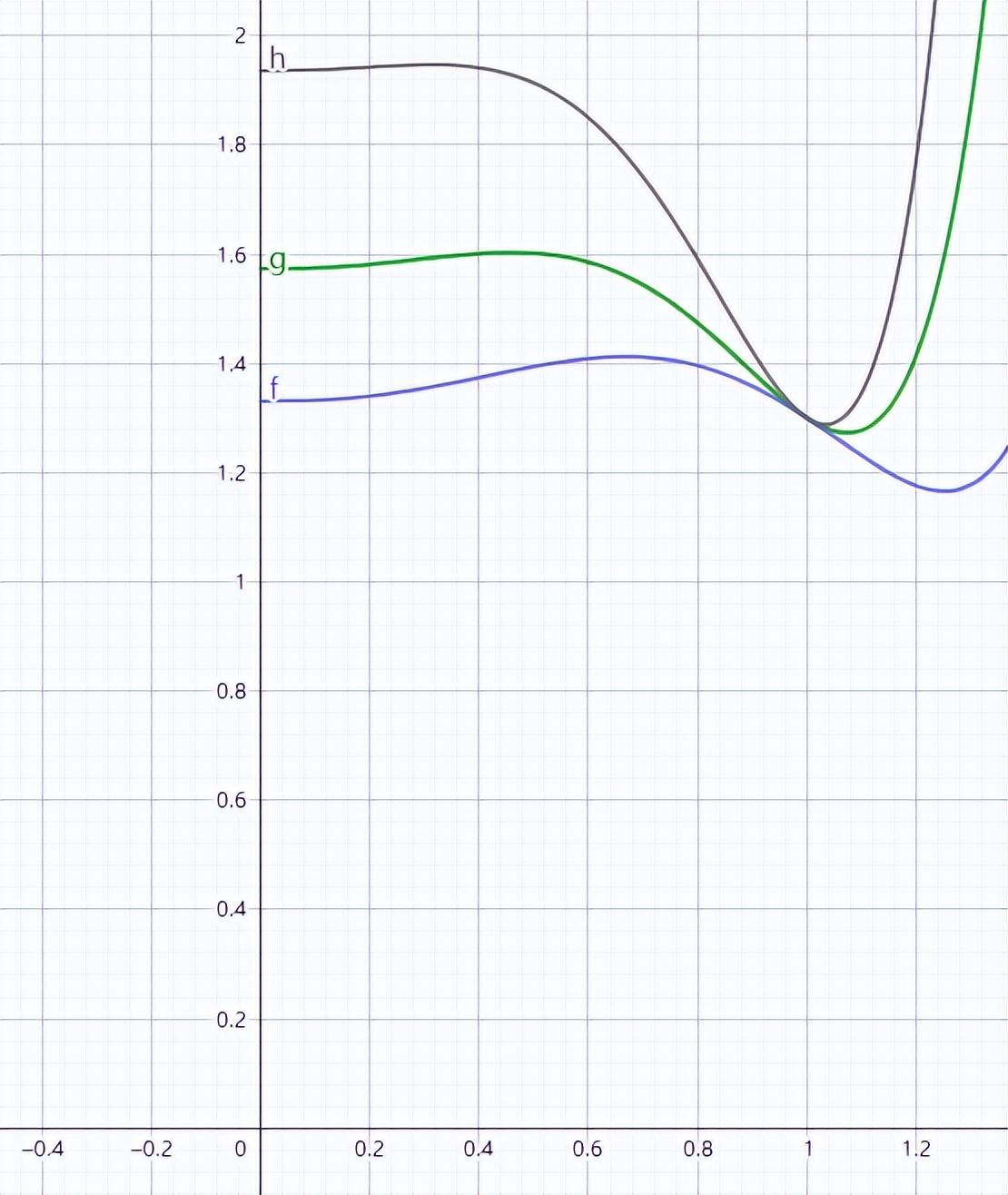
圖4：不同重游率對函數的影響

在其它參數不變的情況下，通過模擬不同重游率，我們得到主題樂園A在重游率分別為10%，30%，60%所對應的極值點為0.67，0.46和0.31，隨著重游率的上升，極值點x的取值向0方向移動，也就是說，如果一個主題樂園的重游率越高，相對應的年卡價格就應該越高，反之，如果重游率越低，所對應的年卡價格應該越低。

（2）非年卡客群人均二消參數β1高低對擬合函數的影響

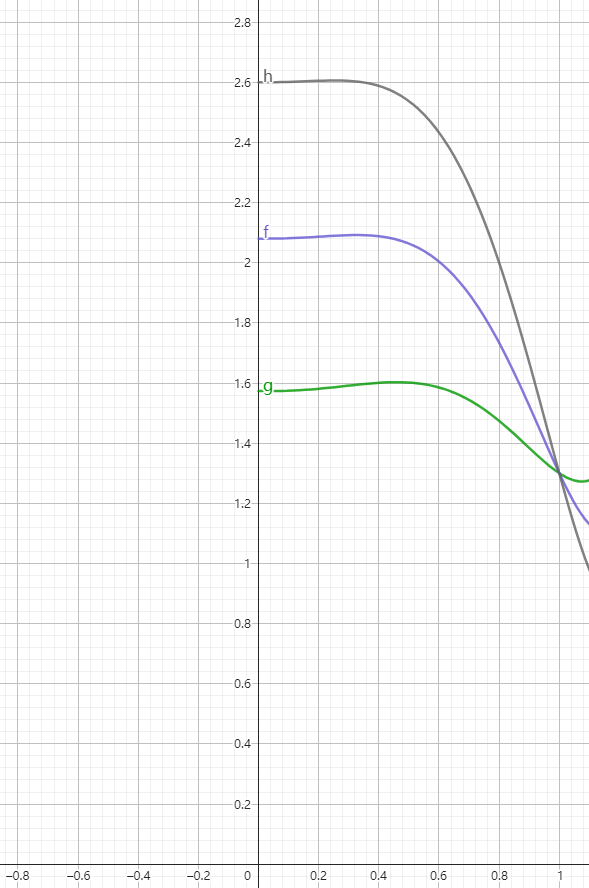
圖5：參數β1高低對擬合函數的影響

參數β1代表非年卡用戶在園區的消費與門票價格的比值，在其它參數不變的情況下，通過模擬不同β1值，我們得到主題樂園A在β1值分別為20%，60%，100%所對應的極值點為0.67，0.33和0.25，隨著β1值的上升，極值點x的取值向0方向移動，也就是說，如果一個主題樂園的非年卡用戶的消費越高，相對應的年卡價格就應該越高，反之，如果消費越低，所對應的年卡價格應該越低。

（3）年卡人均消費β2和使用頻次F對擬合函數的影響

在F(X)函數中，β2和F值兩個參數為乘積關系，所以我們可以使用β2*F的值進行統一分析：

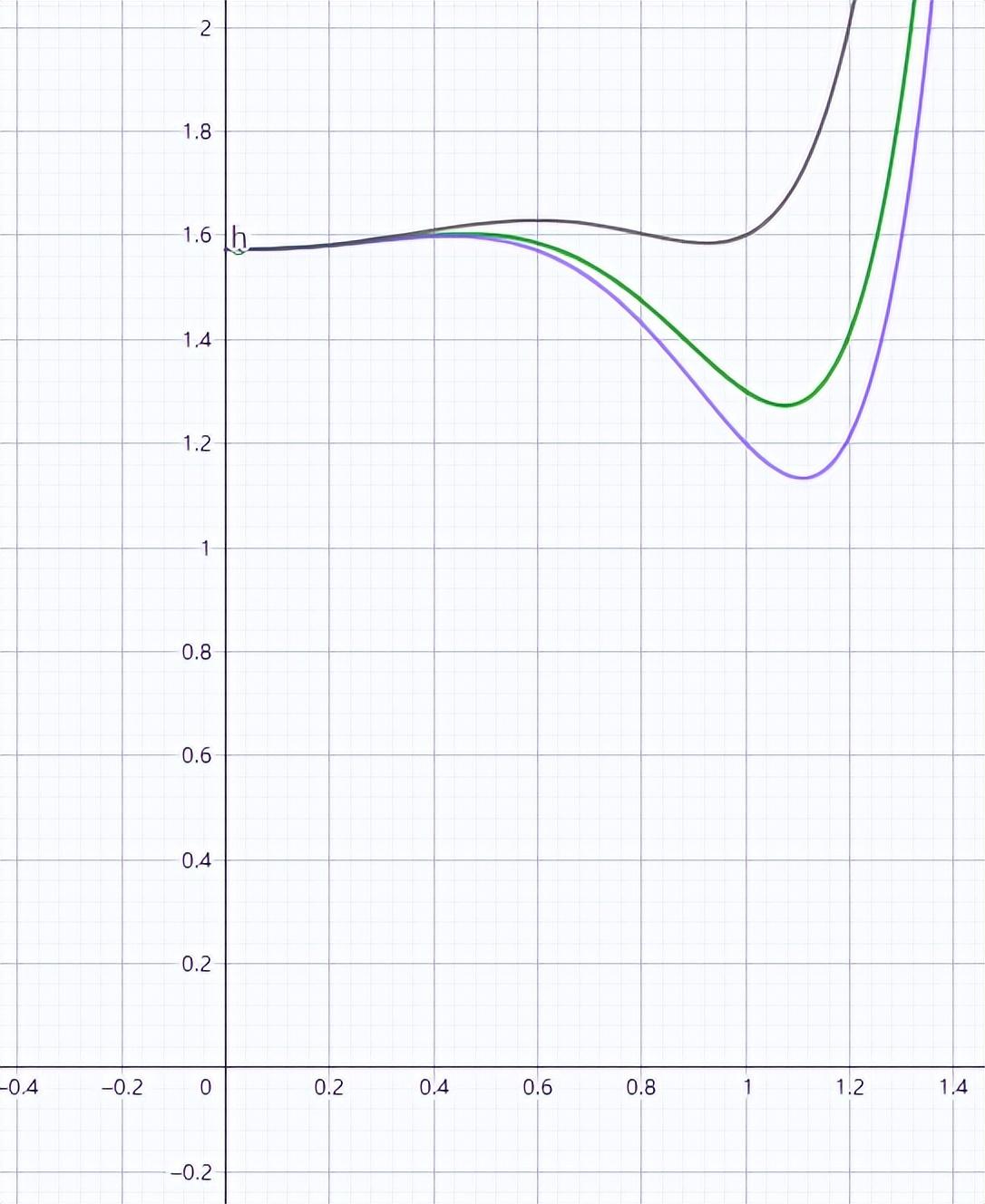
圖6：不同年卡參數（F*β2）對函數的影響

參數F*β2代表著年卡客群在園區消費能力的高低，在其它參數不變的情況下，通過模擬不同F*β2值，我們得到主題樂園A在F*β2值分別為0.2，0.3，0.6所對應的極值點為0.43，0.46和0.59，隨著F*β2值的上升，極值點x的取值向1方向移動，也就是說，如果一個主題樂園的年卡用戶每一次在園區消費越高，相對應的年卡價格就應該越低，反之，如果消費越低，所對應的年卡價格應該越高。

3、擬合曲線形狀對實際年卡定價的啟示

按照上面的模型，一般來說，一個主題樂園（通過調研和數據收集）只要確定了模型中的相關參數，對于既定的門票和游客人數，我們就能夠計算出令樂園收入最大化的年卡價格，但是，在實際工作當中，有很多數據是需要多年積累的，特別是確定變量x和f(x)相關關系的樣本數據，如果是一個新開業的主題樂園，基本是沒有這些數據積累的；其次，很多參數（如一年重游率，二消指數等）由于實際調研過程中，樣本收集和數據收集的工作質量參差不齊，也可能導致相關參數的準確性存在偏離。在這些情況下應該如何應對呢？我們可以從擬合函數的形狀出發進行分析：

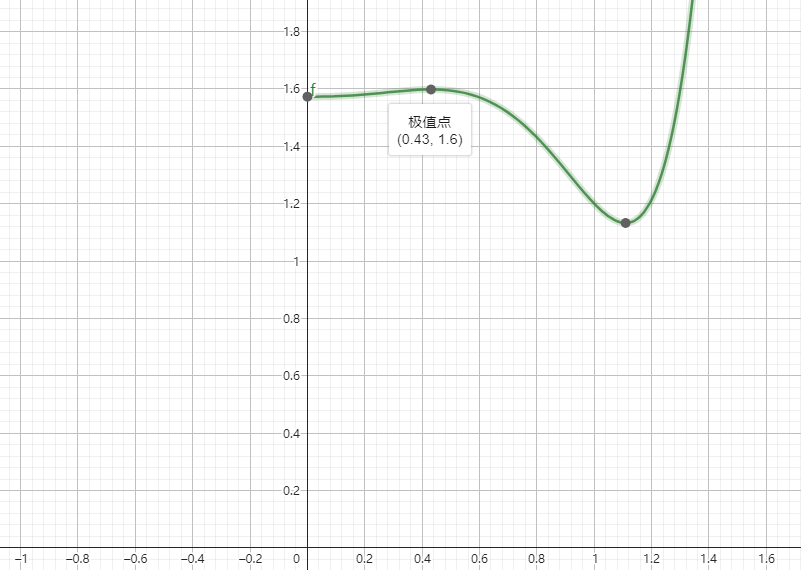
圖7：擬合函數的形狀

圖7是一個典型的F(x)函數曲線，它代表著不同x的取值對于收入高低的影響，x值越接近0，年卡的相對價格越高，x值越接近1，年卡的相對價格越低。我們看到，x值在0到極值點（上圖為0.43）的區間，曲線是相對平緩的，對過了極值點之后，曲線變得陡峭并往下走。而且通過模擬測算我們發現，不同的參數取值對于曲線的形狀影響是比較小的。這意味著，只要是在0到極值點這個區間，對應的總收入變化并不會很大，在這個區間進行年卡價格的制定，總收入是有保證的，但是過了極值點，隨著x的增大，總收入會受到很大的影響，如果在極值點到1這個區間定價，總收入很有可能會受到很大的影響。因此，如果一個主題樂園在數據收集并不準確或并不充分的情況下，可以選擇盡量“貴一些”，這個區間是相對能夠保證收入的安全區間。

實證分析

按照前文的方法，通過建立F(x)函數模型，我們就可以精確計算出收入最大化的年卡和門票價格比值，對于目前國內大部分主題樂園，x值集中在0.2-0.5區間，而且，吸引力越強，重游率越高的樂園，x值越小，這和我們模型的分析是一致的，見下表：

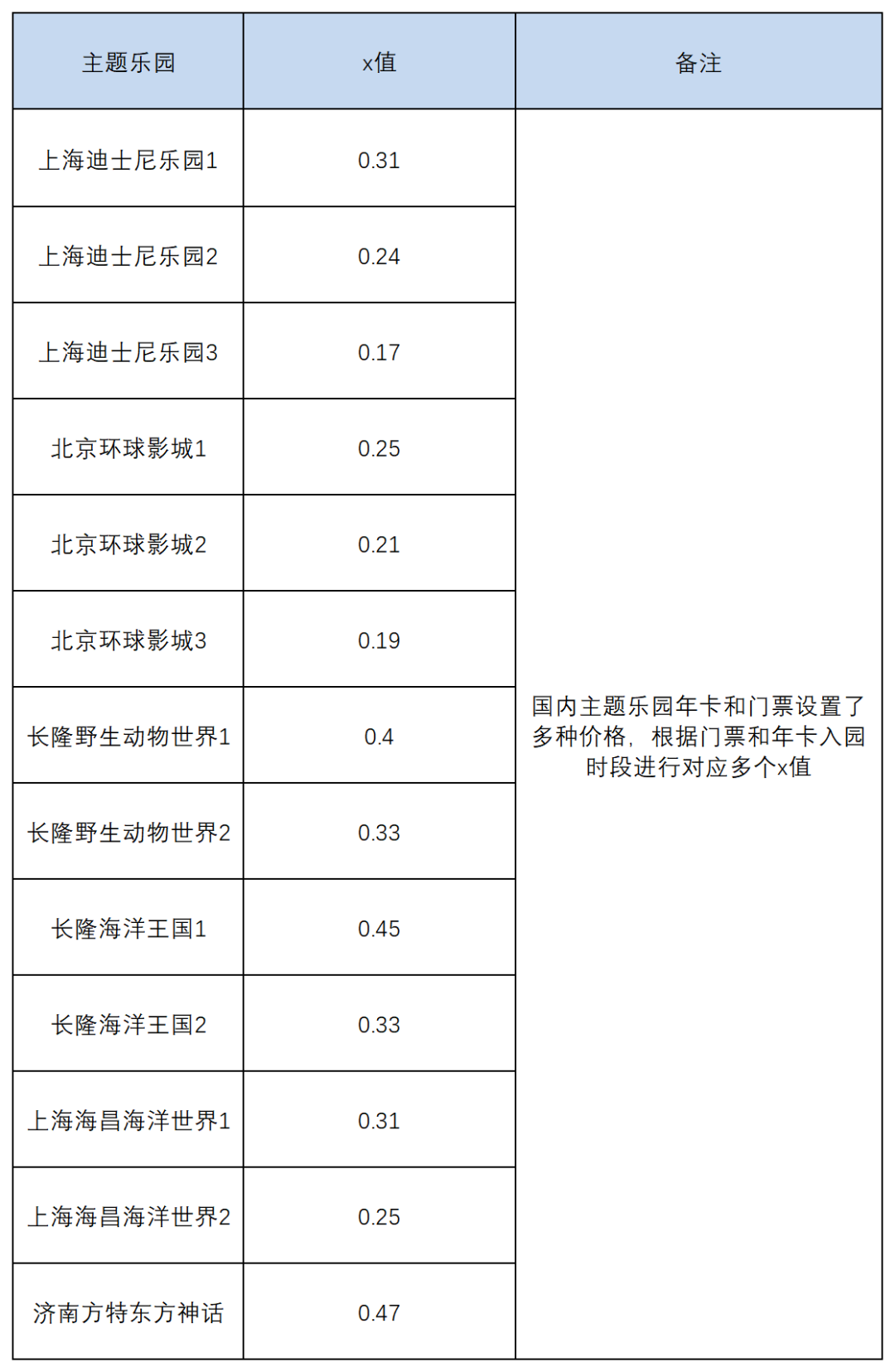
表2：國內部分主題樂園x值

結語

以收入最大化為前提，通過對樣本數據的收集和回歸分析模型，可以得出年卡價格變動如何影響購買年卡的游客的比例的函數關系，進而可以得出年卡價格高低的變動對于總收入的影響的函數關系，從而確定最佳的年卡價格。重游率，二消指數，年卡平均使用頻次等參數取值對于模型極值點有著關鍵影響。在實踐中，如果相關統計數據不夠全面和準確，x取值在（0，極值點）區間是定價的“安全區間”。