▍導(dǎo)讀

近年來，由于在生物醫(yī)療、環(huán)境檢測、化學(xué)分析等領(lǐng)域的廣闊應(yīng)用前景，微流控芯片已成為快速發(fā)展的高新技術(shù)。其中，微混合器是微流控技術(shù)的主要功能器件，為滿足不同濃度溶液快速、完全混合的設(shè)計需求，微流體的驅(qū)動技術(shù)是目前的研究熱點。

電滲驅(qū)動具有驅(qū)動系統(tǒng)結(jié)構(gòu)簡單、操作便捷且無脈動等優(yōu)勢。現(xiàn)有研究電滲流動微混合器大多是通過改變微混合器的結(jié)構(gòu)、電極排布方式、電壓等參數(shù)提高樣品的混合效率，缺乏對電滲流微混合器電極版圖的結(jié)構(gòu)設(shè)計工作。目前，電滲流電極版圖大多基于尺寸優(yōu)化和形狀優(yōu)化的方法進行設(shè)計，難以大幅提升微流控器件性能。

針對上述問題，中國科學(xué)院長春光學(xué)精密機械與物理研究所鄧永波課題組做了長期的研究工作。2018年，課題組針對電滲流電極版圖設(shè)計問題發(fā)展了拓?fù)鋬?yōu)化方法[1]，該方法使材質(zhì)插值可以在Dirichlet和Newman邊界條件之間進行，這是將拓?fù)鋬?yōu)化應(yīng)用在控制本體性能的關(guān)鍵一步。課題組也將該方法進一步推廣，通過拓?fù)鋬?yōu)化進行微泵設(shè)計以獲得更大的凈流量[2]。

近期，針對上述問題的研究又有了新的進展，該課題組孫建文等在《光學(xué) 精密工程》（EI、Scopus，中文核心期刊，《儀器儀表領(lǐng)域高質(zhì)量科技期刊分級目錄》和《光學(xué)和光學(xué)工程領(lǐng)域高質(zhì)量科技期刊分級目錄》“T1級”期刊）上發(fā)表了題為“基于拓?fù)鋬?yōu)化的電滲流微混合器電極”的封面文章。

《光學(xué) 精密工程》2023年第17期封面

▍微混合器模型建立

圖1為電滲微混合器示意圖，作者引入Helmholtz-Smoluchowsk條件將雙電子層進行近似約束處理，通過將模型邊界條件設(shè)置成電勢與電絕緣的插值形式，將電滲流微混合器電極設(shè)計轉(zhuǎn)化成求解插值材質(zhì)分布問題。

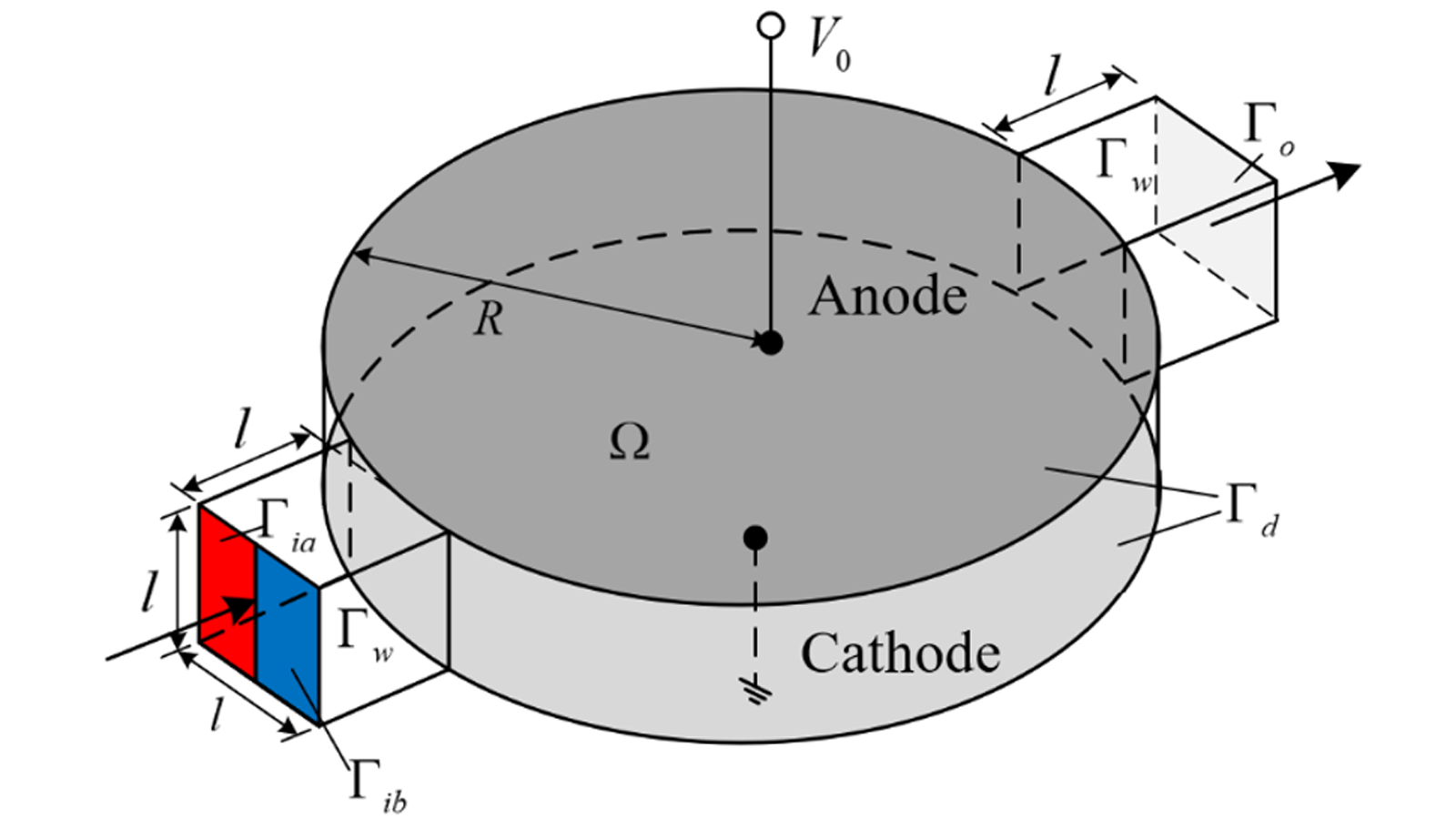
圖1：電滲微混合器示意圖

▍電滲流微混合器混合效果分析

為驗證拓?fù)鋬?yōu)化方法設(shè)計電滲流微混合器電極的可行性，我們對微混合器的混合效果進行分析驗證。在多混合單元的設(shè)計方案下，如圖2所示，兩種不同濃度溶液的混合效果隨混合驅(qū)動路徑增加逐漸疊加，在出口處濃度分布呈現(xiàn)有效混合。數(shù)值實驗結(jié)果表明，所設(shè)計的電滲流微混合器的混合評價指數(shù)在0.05以下，滿足不同濃度溶液完全混合的設(shè)計需求。

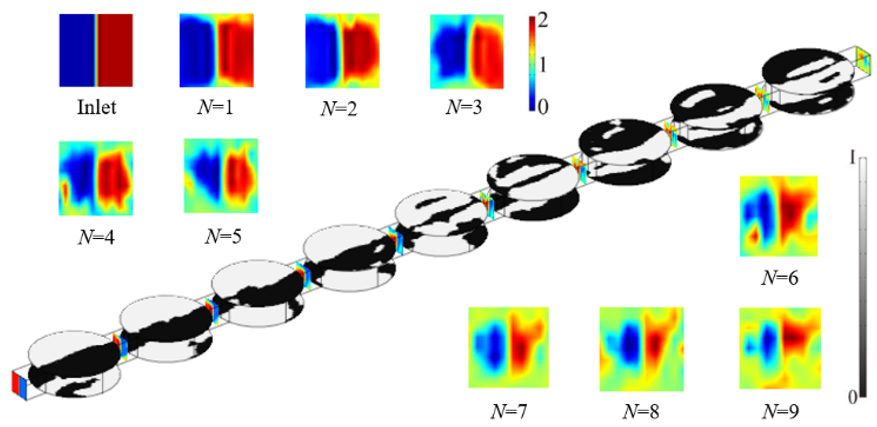
圖2：多混合單元（ N=9）電極版圖和不同混合單元模型方案出口濃度分布

▍研究前景

本文研究基于拓?fù)鋬?yōu)化方法，建立電滲流微混合器模型，設(shè)計優(yōu)化電極版圖。該種電滲流電極設(shè)計方法減少優(yōu)化設(shè)計過程中對設(shè)計者經(jīng)驗的依賴，滿足不同濃度微流體完全混合的設(shè)計需求，在陸空技術(shù)方面有著重要應(yīng)用價值。

▍研究團隊介紹

團隊基于改進的拓?fù)鋬?yōu)化設(shè)計方法設(shè)計微納功能器件，這些器件的研究涵蓋眾多學(xué)科，如光學(xué)、流體力學(xué)等。

在光學(xué)方面，團隊利用拓?fù)鋬?yōu)化研制超構(gòu)透鏡，試圖解決目前超構(gòu)透鏡存在版圖數(shù)據(jù)量大、難以加工、效率低、色差等問題。針對以上問題，團隊利用拓?fù)鋬?yōu)化尋找平衡色散、轉(zhuǎn)換效率的微納單元結(jié)構(gòu)，基于幾何相位設(shè)計了531~ 780 nm的消色差超構(gòu)透鏡，該透鏡在目標(biāo)波段內(nèi)的平均效率達(dá)到53%[3]，顯著優(yōu)于目前同類別的超構(gòu)透鏡。團隊利用拓?fù)鋬?yōu)化設(shè)計的同心納米環(huán)超構(gòu)透鏡，具有低的占寬比，版圖數(shù)據(jù)量小等優(yōu)點。相比已有的設(shè)計方法，同等占寬比的情況下該設(shè)計方法獲得透鏡性能更優(yōu)。基于該方法團隊已經(jīng)研制出口徑為1 mm，數(shù)值孔徑0.8，分辨優(yōu)于600 nm的可見光寬譜超構(gòu)透鏡[4]。針對超構(gòu)透鏡實用化面臨的口徑難以做大的技術(shù)瓶頸問題，團隊基于單元拼接的方法[5]研制了口徑1 cm和2 cm的可見光與紅外超構(gòu)透鏡。口徑1 cm的紅外超構(gòu)透鏡工作波段為8~12 μm，F#為1，分辨率優(yōu)于0.12 lp/mrad，口徑1 cm的可見光超構(gòu)透鏡成像清晰。截至目前，團隊已經(jīng)具備厘米、分米口徑超構(gòu)透鏡的研制能力。

圖3：團隊研制的超構(gòu)透鏡相機樣機與成像結(jié)果

團隊也通過內(nèi)部開發(fā)的拓?fù)鋬?yōu)化算法設(shè)計金屬、介質(zhì)等微納結(jié)構(gòu)用于電磁場增強、光學(xué)異常透射、光學(xué)波導(dǎo)、電磁隱身等相關(guān)應(yīng)用[6-9]。這些研究工作對于在集成光子學(xué)領(lǐng)域中構(gòu)建光學(xué)傳感器件以及利用微納結(jié)構(gòu)操縱和引導(dǎo)光具有指導(dǎo)意義。

在流體力學(xué)方面，團隊提出了基于連續(xù)伴隨分析的流體力學(xué)拓?fù)鋬?yōu)化方法，解決了固液界面紋理的設(shè)計難題，并原創(chuàng)的提出了流形上的拓?fù)鋬?yōu)化方法，將拓?fù)鋬?yōu)化的結(jié)構(gòu)設(shè)計空間擴展到了二維流形上[10-12]。利用以上方法團隊進一步提出了獲取周期性固液界面紋理微結(jié)構(gòu)的嚴(yán)格數(shù)學(xué)模型，通過極小化液汽界面所支撐液體凸起的體積，增強了紋理化固體表面的儲氣能力，這些工作對疏水表面研制和流體力學(xué)減阻具有重要意義[13]。

圖4：表面微納結(jié)構(gòu)及固體表面液體黏附力的對比實驗

團隊已經(jīng)將多年在拓?fù)鋬?yōu)化領(lǐng)域的研究成果整理出版了兩本學(xué)術(shù)專著[14,15]（Adjoint Topology Optimization Theory for Nano-Optics ；Topology Optimization Theory for Laminar Flow），感興趣的讀者可以閱讀。

圖5：團隊出版的兩本拓?fù)鋬?yōu)化領(lǐng)域的學(xué)術(shù)專著

▍論文信息

孫建文, 張健宇, 李博文, 等. 基于拓?fù)鋬?yōu)化的電滲流微混合器電極[J]. 光學(xué)精密工程, 2023,31(17):2515-2524. DOI：10.37188/OPE.20233117.2515.

https://ope.lightpublishing.cn/thesisDetails#10.37188/OPE.20233117.2515

▍作者簡介

鄧永波，中國科學(xué)院長春光機所研究員、博士生導(dǎo)師，入選2018年德國洪堡資深學(xué)者；以第一作者出版Springer英文專著2部；在 CMAME、JCP等權(quán)威期刊和IEEE MEMS、Transducers等領(lǐng)域頂級國際會議上累計發(fā)表論文60篇，獲得授權(quán)中國發(fā)明專利14項；入選2022年中國科學(xué)院穩(wěn)定支持基礎(chǔ)研究領(lǐng)域青年團隊；獲得2016和2017年卡爾斯魯厄理工大學(xué)客座教授獎；入選中國科學(xué)院青年創(chuàng)新促進會會員和IEEE學(xué)會、中國微納技術(shù)學(xué)會等高級會員。

▎參考資料

[1] Deng, Y., et al., Topology optimization of electrode patterns for electroosmotic micromixer. International Journal of Heat and Mass Transfer, 2018. 126: p. 1299-1315.

[2] Sun, J., et al., Topologically optimized electrodes for electroosmotic actuation. Journal of Advanced Manufacturing Science and Technology, 2023. 3(1): p. 2022022-2022022.

[3] Zhang, L., et al., High-Efficiency Achromatic Metalens Topologically Optimized in the Visible. Nanomaterials (Basel), 2023. 13(5).

[4] Jin, Z., et al., Topologically optimized concentric-nanoring metalens with 1 mm diameter, 0.8 NA and 600 nm imaging resolution in the visible. Opt Express, 2023. 31(6): p. 10489-10499.

[5] Wang, C., et al., Fabricable concentric-ring metalens with high focusing efficiency based on two-dimensional subwavelength unit splicing.Opt Express, accepted.

[6] Deng, Y. and J.G. Korvink,Topology optimization for three-dimensional electromagnetic waves using an edge element-based finite-element method. Proc Math Phys Eng Sci, 2016. 472(2189): p. 20150835.

[7] Lin, Y., et al., Topologically optimized periodic resonant nanostructures for extraordinary optical transmission [Invited]. Optical Materials Express, 2021. 11(7): p. 2153-2164.

[8] Han, Y., et al., Nanoantennas Inversely Designed to Couple Free Space and a Metal-Insulator-Metal Waveguide. Nanomaterials (Basel), 2021. 11(12): p. 3219.

[9] Chen, Y., et al., Topology Optimization‐Based Inverse Design of Plasmonic Nanodimer with Maximum Near‐Field Enhancement. Advanced Functional Materials, 2020. 30(23).

[10] Deng, Y., Z. Liu, and Y. Wu, Topology optimization of steady and unsteady incompressible Navier–Stokes flows driven by body forces.Structural and Multidisciplinary Optimization, 2012. 47(4): p. 555-570.

[11] Deng, Y., et al., Topology optimization of steady Navier–Stokes flow with body force. Computer Methods in Applied Mechanics and Engineering, 2013. 255: p. 306-321.

[12] Deng, Y., Z. Liu, and J.G. Korvink, Topology optimization on two-dimensional manifolds. Computer Methods in Applied Mechanics and Engineering, 2020. 364: p. 112937.

[13] Deng, Y., et al., Inversely designed micro-textures for robust Cassie–Baxter mode of super-hydrophobicity. Computer Methods in Applied Mechanics and Engineering, 2018. 341: p. 113-132.

[14] Deng, Y., Adjoint Topology Optimization Theory for Nano-Optics. 2022, Singapore: Springer, Singapore.

[15] Deng, Y., Y. Wu, and Z. Liu, Topology optimization theory for laminar flow. Springer Singapore, Singapore, 2018. 10: p. 978-981.

閱讀原文