三次？遠遠不夠

永遠不要以為，洗個兩三次就能把牌洗開了。很多撲克牌小魔術就利用了三次洗牌遠遠不能把牌洗開的秘密。比方說，我拿出一副新牌給你，由你來負責洗牌。洗一次。再洗一次。你覺得還沒洗開對吧，那就再洗一次。然后，請你偷偷看一眼最上面的那張牌，記下它的花色和點數，然后把它插到這摞牌中間某個位置去，再把整副牌給我。我便能挑出這張被動過的牌。

圖源：pixabay

其實完全不需要特別的作弊方式。魔術的原理正如上文所說：把一摞排列有序的牌洗三遍，并不會讓整副牌完全無序，排列順序會有一個很強的規律。移動最上面一張牌的位置會破壞掉這個規律，從而露出馬腳來。

為了更方便地做進一步說明，我們下面只用 13 張牌來舉例。由于這是一副新牌，初始時這 13 張牌是有序的：

假設洗一次牌，是規律的把上面這個序列分成前后兩半，然后交錯構成一個新的序列：

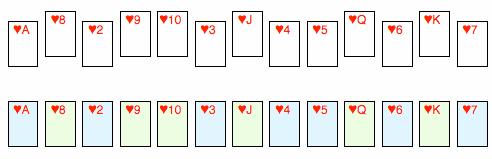
那么洗完一次牌后，依次尋找 A, 2, 3, ...…, J, Q, K 的位置，你會發現它們形成了兩個“上升序列”（分別用兩種顏色標了出來）。

那么，再洗一次牌會對這個序列造成什么影響呢？容易看出，第二次洗牌將會把每個上升序列都截成兩半，然后再次相交錯，得到四個上升序列（分別用四種顏色標了出來）：

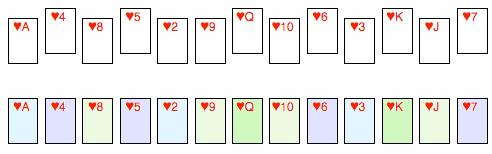
如果此時把末尾的那張 7 移到中間去，你會發現這會打破“四個上升序列”的規律。因此，我們很容易辨認出，在下面的撲克牌序列中，7 本該放在后面：

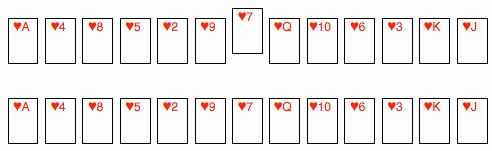
但是在上面的例子中，這些上升序列都很短，理論上平均長度僅為 13 / 4 = 3.25。因此如果對方洗牌技術不佳，魔術就有出錯的可能。不過，如果把 52 張牌洗三次，將產生 8 個上升序列，平均每個上升序列的長度為 52 / 8 = 6.5，魔術表演的問題就不大了。

五次洗牌也洗不均勻

我們可以借助“上升序列”的思路來證明，五次洗牌也不能把牌徹底洗均勻，因為有一些排列永遠不能僅用五次洗牌得到。不妨假設初始時撲克牌的順序是 1, 2, 3, ……, 51, 52，五次洗牌后最多會產生2^5 = 32 個上升序列。但是 52, 51, ……, 3, 2, 1 這個排列中有 52 個上升序列，因此五次洗牌是絕對洗不出這樣的排列的。事實上，所有上升序列數量超過 32 的排列都是五次洗牌無法得到的，這就證明了五次洗牌也不能把牌洗均勻。

看來，要想把牌洗開，六次是必需的了。

七次洗牌才足夠

那么，究竟要洗多少次牌，才能讓所有排列出現的概率大致相同呢？你別說，還真有人做過這樣的研究。

圖源：pixabay

1992 年，佩爾西·戴康尼斯（Persi Diaconis），美國數學家兼專業魔術師，與哥倫比亞大學的戴夫·拜耳（Dave Bayer）一道，為交叉洗牌法建立了一個數學模型，分析了包括上升序列在內的撲克牌排列性質，定義了 m 次洗牌后得到的排列分布與平均分布之間的“總變差距離”，最后發表了一篇 20 頁長的論文。他們計算出，當撲克牌有 52 張，洗牌次數分別為 1, 2, ...…, 10 時，總變差距離分別為 1.000, 1.000, 1.000, 1.000, 0.924, 0.614, 0.334, 0.167, 0.085 和 0.043。可見，五次洗牌才能讓整副牌呈現出隨機性，直到第七次洗牌才會讓隨機性顯著增加；并且在此之后，總變差距離將大致以 1/2 的比例依次遞減。因而他們的結論就是：七次洗牌才足夠隨機。

他們還對這個問題進行了漸近意義上的分析：當 n 足夠大時，需要的洗牌次數大約為 3 log2n / 2。

如果你不是要變魔術而只想玩游戲，建議開一盒新牌之后來個漫天花雨，然后撿起來，可保萬無一失……

作者：matrix67

一個AI

這樣說來，還是老祖宗機智。

本文來自果殼，未經授權不得轉載.

閱讀原文