“問題是，我們到底是生活在哪個（數論）宇宙里？”

一個有零點，一個無零點。

在美籍華裔數學家、加州大學圣塔芭芭拉分校教授張益唐公開其關于朗道-西格爾零點猜想（the Landau-Siegel zeros conjecture）的最新研究論文前，這一零點將數論分成了上述兩個宇宙。

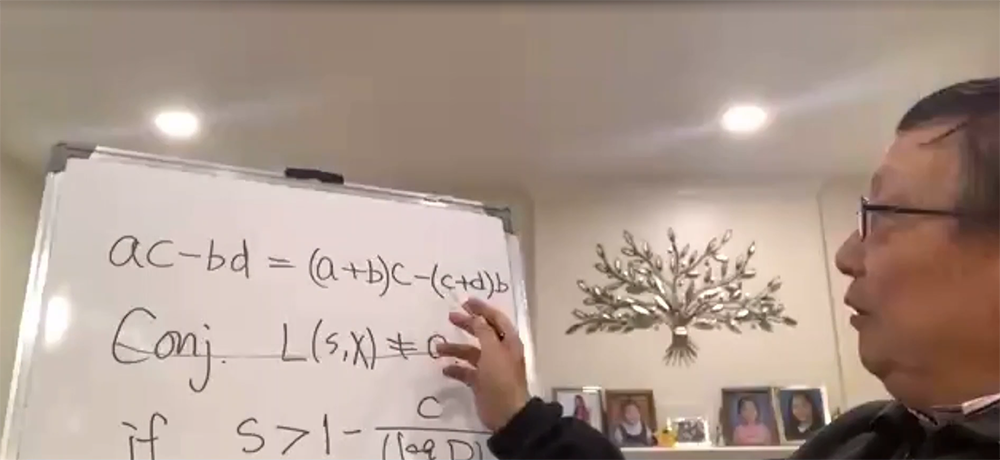
張益唐教授11月8日上午面向北京大學師生和社會公眾關于朗道-西格爾零點猜想的演講

因為不知道這一零點到底存在不存在，數論學家們只好去討論兩種情況：如果這一零點存在，會得出什么結論？如果它不存在，會得出什么結論？

在三天前面向山東大學師生的演講和11月8日上午面向北京大學師生和社會公眾的演講中，張益唐教授都多次提及其最新論文中證明朗道-西格爾零點猜想的創新思想或“New idea”（新方法）。

他同時表示，其論文還需要修改補充，更關鍵的是，要簡化。新研究成果會對代數數論中的二次域的類數問題給出一個非常強的結果。

張益唐教授還在演講中再次提及“大海撈針”。他說，與自己2013年發表的關于孿生素數猜想的研究突破相比，證明朗道-西格爾猜想才是真正的大海撈針。

11月8日上午，對于張益唐在演講中提到的證明朗道-西格爾零點猜想的“New idea”（新方法），全程聆聽該講座的北京大學數學科學學院一位博士后向澎湃新聞（www.kxwhcb.com）解釋稱，最簡略地來講，他是把計算中的z(n）序列，替換成了a(n)、b(n) 、c(n) 、d(n)序列，然后用柯西不等式推出矛盾，證明了在特定范圍內不存在朗道-西格爾零點。

這位博士后進一步解釋說，具體來說，張益唐教授在演講中舉了個例子，對于實連續函數來說，兩個連續的零點之間函數取值是同號的，這樣要證明零點在某個局部存在就等價于證明兩個局部端點的函數值乘積非正，如果構造一個序列x(n)刻畫出零點正負性的特征，那么證明x(n)中某一項為負就說明零點存在。同樣的考慮實本原特征的狄利克雷L函數（當特征是平凡時，即黎曼ζ函數），它的零點存在，也需要證明對于某個序列x(n)，其中一項為負。傳統的方法是，取一組實的z(n)，考慮x(n)(z(n))^2的求和，如果為負，那么x(n)必存在一項為負。但傳統的方法無法從一個無窮小量ε（epsilon）突破到0。張益唐教授的方法是，用a(n)、b(n)、c(n)、d(n)做兩組求和，同時逼近；再使用柯西不等式，推出其中大小關系。這個工作的價值在于，將L(1,χ)的下界從無實效（not effective）的D的負ε次方，改進成實效（effective）的log D的負常數次方。

在演講后的提問環節，有人問說，您所介紹的這種new idea，是看著“初等”，實際上是從非常深的工作中才提煉出來的，還是說是在大海撈針之后，直接用了一個初等的 idea去指導工作？

張益唐在回答這個問題時表示，“我的論文當然還要做很多修改和補充。可能更關鍵的是，要簡化。否則的話，確實（令人）比較頭疼。”

11月6日，菲爾茲獎得主詹姆斯·梅納德（JamesMaynard）攻讀博士學位時的導師、致力于解析數論領域的英國數學家、牛津大學數學研究所退休教授羅杰·希思-布朗（Roger Heath-Brown FRS）向澎湃新聞表示，“好好研讀（張益唐的）這篇論文需要很長時間，所以我現在還不能說它是否正確。但它寫得很清楚，而且策略明智。”

張益唐在演講中說，“有的時候你說你用到了一些高深的東西，實際上從范圍來講，也沒有超出復變函數的范圍，但它有它的特殊處理方法。有些東西被弄得非常細膩，非常精致，所以它是一整套（方法）。就像我這個論文里，其實也有很多（這樣的特殊處理方法）。最后有些東西我可能以后還得把細節補出來。有一些算術、有一些特殊的一些‘和’，我能夠知道它的結果（的），基本上我也就給出聲明了。但很多細節，現在說起來，寫這些東西，對我來講，還是很頭疼了。”

張益唐表示，“這里嚴格講起來，每一步都應該說都是初等的，但真正z(n)的選擇，而且最后你要能夠算出那個和，那就需要用到很多解析的工具。”

他還以菲爾茲獎得主塞爾伯格的研究為例稱，“有時候初等比解析的東西更難，更有挑戰性。”

還有人問起，關于朗道-西格爾猜想的研究突破在數論或算數幾何中會有哪些應用？

張益唐回答，在數論里，它至少解決了一個目前為止還懸而未決的問題——“素數在等差級數中的分布”。“（如果）可能存在朗道-西格爾零點的話，那么在某些等差級數里，素數會特別多；在某些里頭，素數會很少。我這個結果出來以后，至少把這個問題解決了。”

張益唐說，“在應用里頭，因為是牽扯到解析數論，什么地方都得用到這個（結果）。”“還有一個，是代數數論里二次域的類數問題，這會給出一個非常強的一個結果。”

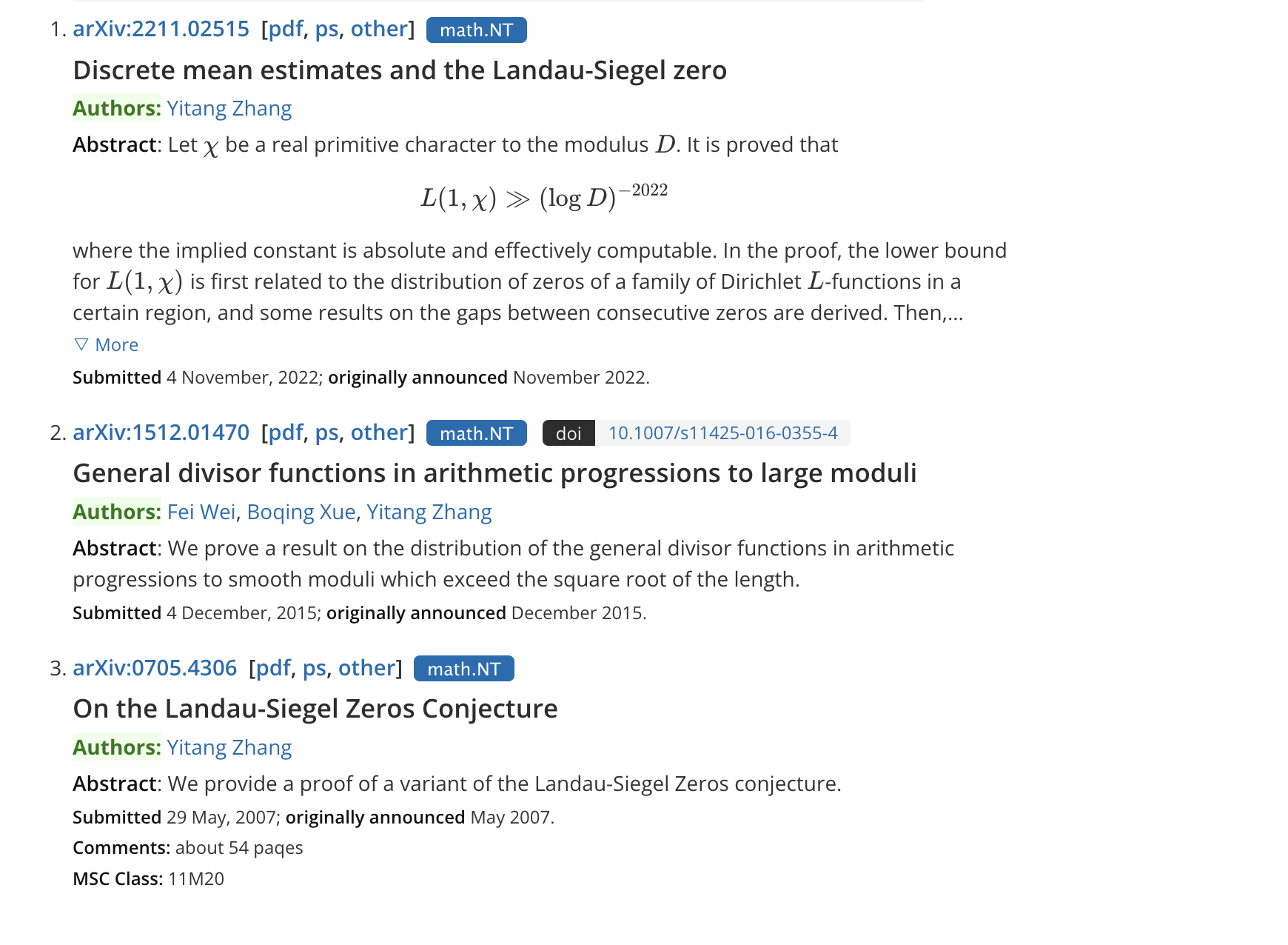
張益唐在網站arXiv上公開的三篇預印本論文

張益唐于2013年4月17日在《數學年刊》（Annals of Mathematics）發表《素數間的有界間隔》，首次證明了存在無窮多對素數對（p, q），其中每一對素數之差，即p和q的距離，不超過7000萬。這為世紀難題“孿生素數猜想”的解決做出了突破性工作，他從一位默默無聞的大學講師躋身世界重量級數學家的行列。隨后，“7000萬”這一數字，被數學界同行改進到600和246。

2007年5月29日，張益唐就曾在預印本網站arXiv提交了一篇標題為《論郎道-西格爾零點猜想》（On the Landau-Siegel Zeros Conjecture）的論文。該論文一共54頁，正文13小節。該論文稱，“我們提供了朗道-西格爾零點猜想的一個變體的證明。” 

15年后，張益唐再次發布關于朗道-西格爾零點猜想的論文。在內部流出兩天后，2022年11月7日，其最新論文在預印本網站arXiv上正式對外公開。論文的標題是《離散均值估計和朗道-西格爾零點》（Discrete mean estimates and the Landau-Siegel Zero）。全文111頁，正文18個小節。

11月6日上午11:05，山東大學微信公眾號發布了山東大學數學學院教授、博士生導師、原數學學院副院長、山東大學澳國立聯合理學院執行院長呂廣世、山東大學數據科學研究院教授、博士生導師黃炳榮等人聯合撰寫的文章。

該文章稱，張益唐教授介紹了他在朗道-西格爾零點猜想研究方面的創新思想，在其最新預印本論文里證明了：模D的實原特征L-函數在區間（1?c(log D)^?2024,1】內沒有實零點。

“如果把這里的2024換成1，就得到原始形式的朗道-西格爾零點猜想。2024雖然大于1，但在數學意義上，與1并沒有實質性的差別。”山東大學微信公眾號上述文章稱。

20多天前，在美東時間10月14日下午8時（北京時間10月15日上午8時）舉行的北京大學大紐約地區校友會的活動中，張益唐提前宣布了已解決朗道-西格爾零點猜想問題的消息。他說，要解決這一問題，最后歸結到要做一個不等式；就是要構造一組數。“有人說孿生素數猜想是大海撈針，其實朗道-西格爾零點才是大海撈針。這些年來我試了無數種（情況），試數給代進去， 我建立了一整套公式，所以能去算。我試了無數種情況，每一次都差一個 ε（音：伊普西龍）。”

他說，他把“海底”查遍了，最后發現，不要這根針也能解決這一零點猜想問題。“我敢肯定地說，我做出來了。我知道我這么做是對的。”

在11月8日上午的演講中，張益唐表示，在本質上，他已經證明了朗道-西格爾零點猜想。只是像他此前關于孿生素數猜想的研究結果一樣，其結果可以被改進。這一最新研究突破將有很多應用，帶來很多定理。

換句話說，張益唐的最新論文表明，在特定范圍內，朗道-西格爾零點不存在。在這一情況下，朗道-西格爾零點猜想正確或成立。

“朗道-西格爾零點”被定義為廣義黎曼猜想的反例。斷言“朗道-西格爾零點”不存在的猜測，被稱為朗道-西格爾零點猜想。

張益唐在演講中同時表示，目前他把朗道-西格爾零點猜想的證明相關指數做到了2024，“比較慶幸。”這一結果可以被改進，但指數2024可以被改進到什么程度？“我想至少可以弄到幾百吧。但弄到1？我的辦法還是不夠。”

張益唐教授的這一最新成果引起了數學界和社會公眾的極大關注。這會不會成為其數學研究中的又一重要突破？有待數學界專家們的確認。