美籍華裔數(shù)學家、加州大學圣塔芭芭拉分校教授張益唐

澎湃新聞（www.kxwhcb.com）獲悉，在內(nèi)部流出兩天后，11月7日，美籍華裔數(shù)學家、加州大學圣塔芭芭拉分校教授張益唐關(guān)于郎道-西格爾零點猜想（the Landau-Siegel Zeros Conjecture）的最新論文在預(yù)印本網(wǎng)站arXiv上正式對外公開。

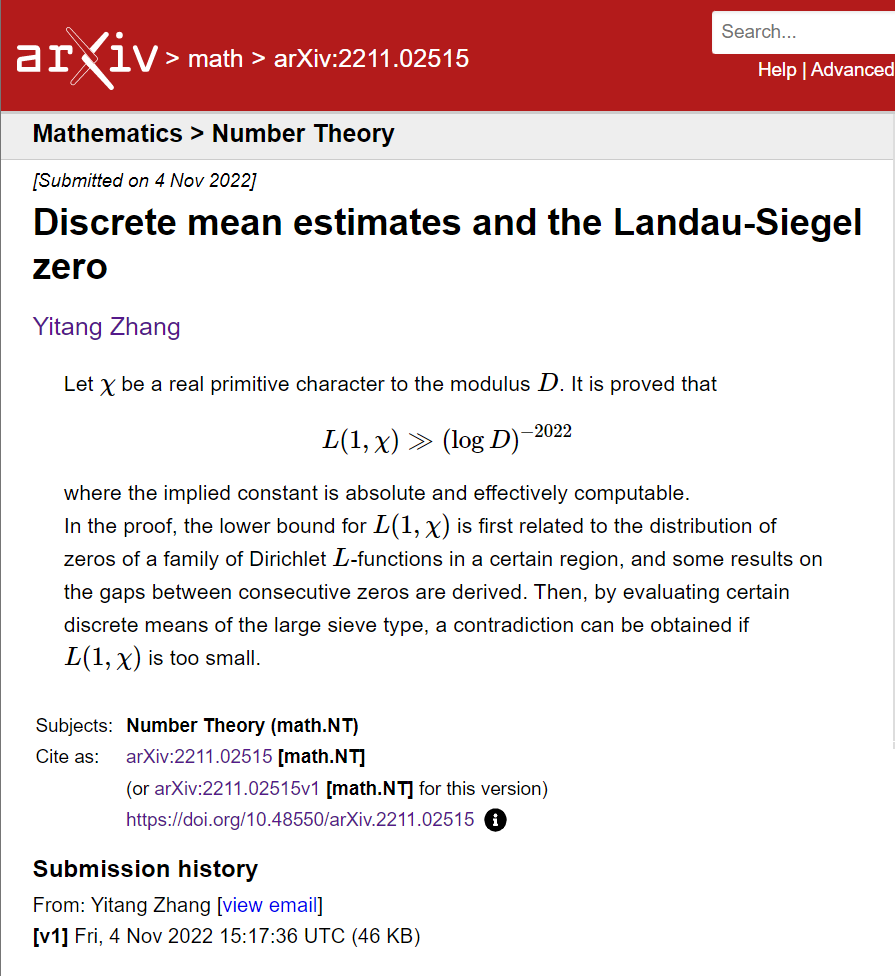
張益唐關(guān)于郎道-西格爾零點猜想的最新論文正式對外公開

該網(wǎng)站顯示，上述論文于當?shù)貢r間2022年11月4日15:17提交至該網(wǎng)站，其PDF文件大小577KB，全文111頁，正文18個小節(jié)，并公布了兩個定理。

論文的標題是《離散均值估計和朗道-西格爾零點》（Discrete mean estimates and the Landau-Siegel Zero）。

澎湃新聞注意到，這一論文的標題，與張益唐教授2021年12月10日在日本慶應(yīng)義塾大學理工學部學術(shù)報告時的主題僅一詞之差。后者為《離散均值公式和朗道-西格爾零點》（Discrete mean formulas and the Landau-Siegel zero）。

對于張益唐的上述論文，國際學術(shù)同行怎么看？

11月6日，菲爾茲獎得主詹姆斯·梅納德（JamesMaynard）攻讀博士學位時的導(dǎo)師、致力于解析數(shù)論領(lǐng)域的英國數(shù)學家、牛津大學數(shù)學研究所退休教授羅杰·希思-布朗（Roger Heath-Brown FRS）向澎湃新聞表示，“好好研讀這篇論文需要很長時間，所以我現(xiàn)在還不能說它是否正確。但它寫得很清楚，而且策略明智。”

對于自己的證明，張益唐教授信心滿滿。20多天前，在美東時間10月14日下午8時（北京時間10月15日上午8時）舉行的北京大學大紐約地區(qū)校友會第十期“未名傳承系列活動”上，張益唐表示，“我最近在數(shù)學上又作出了一個應(yīng)該說是很大的成果。可以說是弱一點的形式，但本質(zhì)上已經(jīng)是解決了朗道-西格爾零點（猜想）問題。解析數(shù)論的同行會知道，這個問題的解決，可能比孿生素數(shù)猜想的意義更大。”

“我敢肯定的說，我做出來了。我知道我這么做是對的。”張益唐在上述活動的在線報告中說。

朗道-西格爾零點猜想被認為是廣義黎曼猜想的一種特殊并且可能比其弱得多的形式。它斷言“朗道-西格爾零點”不存在。“朗道-西格爾零點”被定義為廣義黎曼猜想的反例。

11月5日上午，張益唐教授就上述研究的新突破向山東大學師生作了線上學術(shù)報告。

一天后，11月6日上午11:05，山東大學微信公眾號發(fā)布了山東大學數(shù)學學院教授、博士生導(dǎo)師、原數(shù)學學院副院長、山東大學澳國立聯(lián)合理學院執(zhí)行院長呂廣世、山東大學數(shù)據(jù)科學研究院教授、博士生導(dǎo)師黃炳榮等人聯(lián)合撰寫的文章。

該文章稱，張益唐教授介紹了他在朗道-西格爾零點猜想研究方面的創(chuàng)新思想，在其最新預(yù)印本論文里證明了：模D的實原特征L-函數(shù)在區(qū)間（1?c(log D)^?2024,1】內(nèi)沒有實零點。

“如果把這里的2024換成1，就得到原始形式的朗道-西格爾零點猜想。2024雖然大于1，但在數(shù)學意義上，與1并沒有實質(zhì)性的差別。”山東大學微信公眾號上述文章稱。

但這是否意味著，張益唐在實質(zhì)上已經(jīng)證明了朗道-西格爾零點猜想？有待數(shù)學界專家們的確認。

山東大學微信公眾號上述文章稱，“如果我們相信廣義黎曼猜想，那么朗道-西格爾零點應(yīng)該不存在。朗道-西格爾零點的研究非常重要，是解決很多數(shù)論問題的瓶頸。所謂的朗道-西格爾零點猜想斷言，朗道-西格爾零點確實不存在。這是數(shù)論中長期懸而未決的重要猜想。一旦證明了朗道-西格爾零點猜想，就可以取得很多新突破，簡化和加強很多經(jīng)典數(shù)論結(jié)果。”“素數(shù)分布一直是數(shù)論研究的中心問題…… 正如黎曼zeta函數(shù)的零點分布與素數(shù)分布之間有著深刻密切的聯(lián)系，狄利克雷L-函數(shù)零點分布也在素數(shù)理論中發(fā)揮廣泛而根本性的作用，與素數(shù)分布的諸多核心問題有著深刻的內(nèi)蘊聯(lián)系，如哥德巴赫猜想、孿生素數(shù)猜想等。”

在山東大學的講座中，張益唐等人隨后圍繞中國數(shù)論學派的傳統(tǒng)與對原始創(chuàng)新的不懈追求，中國數(shù)論學派的研究特色和優(yōu)勢，以及數(shù)論研究的發(fā)展等話題進行了深入探討。張益唐教授談到，數(shù)論在任何時候都是有發(fā)展前途的，嚴謹治學的風格、鍥而不舍的精神非常重要，經(jīng)典方法是否有效，取決于你是否能把它做到極致。

在上述北京大學大紐約地區(qū)校友會的活動中，張益唐說，解決朗道-西格爾零點猜想問題，最后歸結(jié)到就是做一個不等式；就是要構(gòu)造一組數(shù)。“有人說孿生素數(shù)猜想是大海撈針，其實朗道-西格爾零點才是大海撈針。這些年來我試了無數(shù)種（情況），試數(shù)給代進去， 我建立了一整套公式，所以能去算。我試了無數(shù)種情況，每一次都差一個 ε（音：伊普西龍）。”

張益唐于2013年4月17日在《數(shù)學年刊》（Annals of Mathematics）發(fā)表《素數(shù)間的有界間隔》，首次證明了存在無窮多對素數(shù)對（p, q），其中每一對素數(shù)之差，即p和q的距離，不超過7000萬。這為世紀難題“孿生素數(shù)猜想”的解決做出了突破性工作，他從一位默默無聞的大學講師躋身世界重量級數(shù)學家的行列。

大海撈針想要解決朗道-西格爾零點猜想問題的張益唐稱，他把“海底”查遍了，最后發(fā)現(xiàn)，不要這根針也能解決這一零點猜想問題。

他說，“最早1837年狄利克雷開始研究這個問題，那也將近200年了……始終差一個ε（音：伊普西龍），始終就是沒法突破。但應(yīng)該說，我還是突破了，最后我把它給做成了。”

被提前內(nèi)部流出的張益唐的最新論文在知名社交論壇 Reddit上也被網(wǎng)友熱議。在知名數(shù)學互動網(wǎng)站mathoverflow上，有網(wǎng)友問，假設(shè)張益唐的證明是正確的，那么，接下來會有哪些著名的數(shù)論結(jié)果？

微信公眾號“ 普林小虎隊”援引相關(guān)信源稱，張益唐的同事、曾說過“如果張益唐能夠證明朗道-西格爾零點猜想，就相當于一個人被閃電擊中兩次”的解析數(shù)論專家Jeffrey Stopple指出，張益唐的成果能夠用來研究歐拉和高斯遺留下來的一個關(guān)于“方便數(shù)”（idoneal number）的問題，把它化為有限次計算。當然，所有一切都建立在張益唐論文是正確的基礎(chǔ)之上。

在北京“未來科學大獎周2019”上，張益唐表示，在很多研究方面，因為我們不知道郎道-西格爾零點到底存在不存在，于是數(shù)論學家們就只好去討論兩種情況：如果它存在，會得出什么結(jié)論？如果它不存在，會得出什么結(jié)論？“如果這個零點真存在，不得了！廣義黎曼假設(shè)就錯了……我們會得到很多的推論，而且是非常強的推論，甚至強的有點過頭了。”

15年前，2007年5月29日，張益唐就在預(yù)印本網(wǎng)站arxiv提交了一篇標題為《論郎道-西格爾零點猜想》（On the Landau-Siegel Zeros Conjecture）論文稱，“我們提供了朗道-西格爾零點猜想的一個變體的證明。”但據(jù)說證明過程存在問題。

而這一次，人們希望張益唐取得數(shù)學研究上的又一個重要突破。

北京大學、北京大學數(shù)學科學學院、北京國際數(shù)學研究中心等微信公眾號11月5日下午發(fā)布消息稱，張益唐教授受邀，將于11月8日上午9:00-10:00在線上進行“關(guān)于郎道-西格爾零點猜想”的學術(shù)報告。