我的物理學界同事大多對數學采取功利主義的態度。也許因為受我父親的影響，我較為欣賞數學。我欣賞數學家的價值觀，欽佩數學的優美和力量：它既有戰術上的隨機應變，又有戰略上的深謀遠慮。而且，堪稱奇跡中的奇跡：它的一些美妙概念竟是支配物理世界的基本結構。

楊振寧，《楊振寧論文選集》

我請大家注意楊振寧的三個很突出的、同時也是罕見的集齊于一身的特點。第一，極其高超的數學能力，使他能夠解決技術性問題；第二，對自然的深刻理解，使他能提出重要的問題；第三，一種團隊精神，使他在中國文化的復興中發揮主要作用。總之，這三種特質，造就了楊振寧之所以成為楊振寧，一個保守的革命者，他尊重歷史并引領未來。

Freeman Dyson

撰文 | 林開亮

欣逢楊振寧先生百歲華誕之際【編注：楊先生生于1922年農歷八月十一（公歷十月一日）】，我們對楊先生的數理工作略作介紹，希望有助于增進讀者對楊先生非凡的學術成就的了解。首先要聲明，筆者的物理修養不足，這里無法揭示楊先生工作之物理背景，請讀者見諒。為免得讀者誤以為楊先生僅僅是擅長數學而已，這里我要先引用一段話 (參見注釋[2]) :

問：我想您一向認為，理論發展中物理圖像要很清楚，這也是您一貫的風格，是不是理論物理學家的風格也很不一樣？

楊：我想如果把理論物理學家分類，可以有種種的方向來分，我們單講一個方向， 就是對于數學的喜愛、能力以及用數學的風格，由這個方向可以把理論物理學家放在一條在線，一邊是非常數學的，一邊是非常不數學的。

如果我們談到理論物理學家的風格， 可以把當時最要做數學的， 最不要做數學的， 和后來的規范場論， 說成是三個方向， 一個在右， 一個在左， 一個在中間。我一直認為在中間的較容易成功。

圖1：《楊振寧論文選集》收入楊振寧自選的部分代表作，1983年出版。雕塑家熊秉明(1922-2002)[1]為封面題字，其父是數學家熊慶來(1893-1969)。

事實上，楊先生本人就是那種“在中間的”理論物理學家。作為對照，楊振寧在普林斯頓高等研究所的同事Freeman Dyson (1923-2020) 就屬于“最要做數學”的那一種，參見注釋[3]。

一

單位圓定理 [1952]

1952年，楊振寧與李政道合作，研究了相變理論，在第二篇合作文章中，引出了他第一個引以為豪的數學結果，稱為“單位圓定理”。關于該定理的發現過程，楊先生在1983年出版的《楊振寧論文選集》中引用了1969年寫給Mark Kac (1914–1984) 的一封信：

爾后，12月20日左右的一個晚上，我在家里工作，忽然領悟到，如果使Z1，Z2，… 成為獨立變量并研究它們相對于單位圓周的運動，就可以利用歸納法、通過類似于您所用的那種推理得到完整的證明。一旦有了這個想法，只消幾分鐘就可以寫出全部的論證細節。

第二天早上，我開車同李政道去弄棵圣誕樹，在車上我把這個證明告訴了他。稍晚些時候，我們到了研究所[4]。我記得，我在黑板上給您講述了這個方法。

這一切我都記得很清楚，因為我對這個猜想及其證明感到很得意。雖然說這算不上什么偉大的貢獻，但是我滿心歡喜地視之為一顆小珍珠。

圖2：李政道與楊振寧在普林斯頓高等研究所合影，1961年左右。

有跡象表明，這是楊振寧發現的第一個漂亮數學定理。楊振寧的弟弟楊振平 (1930–2018) 曾寫到[5]:

1951年圣誕節，我去普林斯頓大哥家度假，他那時剛剛證明了單位圓定理。我大學尚未畢業，數學和物理的基礎都不是很強，他興致極高地跟我講單位圓定理。雖然我完全不明白他說什么，可是他當時的極端興奮給我留下了不可磨滅的印象。他說他在這個問題上苦思良久沒有結果，曾經去請教高等研究所著名數學家 Von Neumann 教授。Von Neumann 亦不知如何措手。六個星期以后，他終于解決了困難，得到了全部證明。他當時還說，“這恐怕將是我一生中能證明的最美的定理。”多年以后，我提起他的這句話， 他已經完全不記得了， 可能是因為他做了更重要更美的工作。

圖3：楊振寧與Kac Kac以Feynman–Kac公式聞名，在1940年代與P. Erd?s一起將數論概率方法引入

為介紹單位圓定理，我們需要了解圖上的Ising模型。它是磁鐵的一個統計力學模型，由物理學家E.Ising (1900–1998) 在1925年提出。給定一個 (有限) 圖G，它的頂點 (只有有限多個) 集合記為V，邊的集合記為E。表示這些頂點之間的基本關系 (是否有邊相連) 的，是一個鄰接矩陣，記為A。現在假設在每個頂點放置一個磁針，北極可能朝上或朝下，分別用±1表示。這樣一個構型就稱為一個狀態 (state)，它可以用一個函數ω: V→{1, -1}表示，可以視為一個|V|維列向量，這里|V|表示集合V的元素個數，即頂點的個數。所有狀態的集合不妨記為

。對于每個狀態ω，賦予能量

其中h，J是常數，ωT是

的轉置，ηT=(1,…,1)是分量全部為的維行向量 (換言之，η描述的狀態是全部磁針北極朝上) 。這就給出了任意一個圖G上的Ising模型。

根據統計力學的Boltzmann-Gibbs原理，狀態ω出現的概率P(ω)正比于

，其中

，k是Boltzmann常數，而T是溫度。從而有配分函數 (歸一化常數)

將Ising模型的能量函數代入，就得到

做變量替換

，就有

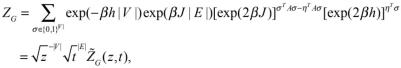
其中|E|是集合的元素個數，即邊的數目，

(對每個給定的t) 是z的|V|次多項式。于是Lee-Yang 單位圓定理相當于說：

定理 1 對任意的圖G上的Ising模型，其約化配分函數

對任意的參數t∈[1, +∞)，其零點落在單位圓周|Z|=1上。

事實上，單位圓定理比定理1更一般。一般的單位圓定理說，同樣的結論 (約化配分函數的零點落在單位圓周) 對實對稱矩陣A成立，只要A的每一個非對角元都非負。

單位圓定理在物理學中有重要意義，引起了許多數學物理學家的興趣，例如T. Asano, M. Suzuki, M. E. Fischer, D. Ruelle,C. M. Newman, E. H. Lieb 與 A. D. Sokal等。

特別值得一提的是，法國高等科學研究所的 Ruelle (1935–) 曾在其科普著作《數學與人類思維》中專辟一章講單位圓定理，并且在給我 (譯者之一) 的郵件中特別提到：“The Lee-Yang theorem remains a gem that I like to revisit from time to time (see for instance in my publications in www.ihes. fr/~ruelle/CVAnglais.html).” 此處，Ruelle 提到的是一篇發表于《數學年刊》的文章：Lee–Yang 多項式的刻劃。此外，1970 年，E. Lieb 與O. J. Heilmann 給出了單位圓定理在圖論中的一個變體：任意圖的匹配多項式 (matching polynomial) 僅有實零點。這一結果及其改進被 A. Marcus, D.Spielman 和 N. Srivastava 用于構造 Ramanujan 圖，其成果發表在 2015 年的《數學年刊》。

晚年時，楊振寧曾提起單位圓定理[6]：

我有個很有名的定理，叫做“單位圓定理”。單位圓定理是說，在物理中很有用的一類多項式，它們的根都在單位圓周上。我之所以會想到考慮多項式的根，是因為在我很小的時候，我父親(按：楊武之，清華大學數學教授)就教給我兩個漂亮的定理，其中之一是代數基本定理，它說每個非常數的多項式有復數根。(另一個是正 邊形可以尺規作圖，恰好與對稱有關）

插話：楊武之的數論工作

楊武之在1928年的博士論文里證明了，每個正整數都可以寫成9個形如

的數之和。這樣的數稱為正四面體數。

圖4：楊武之，1896–1973. 1928 年在芝加哥大學 L. E. Dickson 門下獲得博士學位，將近代代數與數論引入中國，是華羅庚研究數論的引路人

1952年，英國數學家 G.L.Watson (1909–1988) 改進了這一結果，證明了每個正整數都可以寫成8個正四面體數之和。這也是目前最好的結果。但這并非理想的結果，理想的結果是英國數學家F.Pollock (1783–1870) 在1843年提出的下述猜想：每個正整數都可以寫成5個正四面體數之和。Pollock的猜想，是古典的Waring問題的一個變體。以華羅庚、陳景潤為代表的中國數學家在Waring問題上取得了突出成就。關于這些問題的歷史以及新近發展，可見注釋[7]。

二

Yang-Mills規范場論[1954]

楊振寧先生曾經講，他的工作有兩個主題，統計力學與對稱，前者約占三分之一，后者約在三分之二。從源頭上講，它們分別受到碩士論文指導老師王竹溪 (1911-1983) 和學士論文指導老師吳大猷 (1907-2000) 的影響。單位圓定理是他在統計力學的工作，現在我們來介紹他在對稱方面的一項重要工作，這也是他一生最重要的工作——Yang-Mills規范場。

1954年，楊振寧從普林斯頓高等研究所到布魯克海文國家實驗室度學術假，與R. Mills (1927-1999) 共用一個辦公室。楊振寧與Mills分享了關于推廣電磁學的規范不變性原理的嘗試，他們非常幸運地得到同位旋的規范不變性原理，規范場論誕生了。

圖5：楊振寧與 Mills,1999 年在楊振寧退休研討會上的合影

從數學上，大致可以這樣理解。所謂場，就是力場，它通常借助于勢函數描述。例如，對于引力場，萬有引力F可以描述為引力勢函數

的梯度。對于電磁場，場強F也可以用電磁勢函數A來描述，但要略微復雜一些：

楊振寧早年在芝加哥讀博士時，就考慮，如果勢函數A從數變成矩陣B ，那么它的力場該如何寫？他曾嘗試下述看似“自然”的推廣

但由于矩陣的乘積不可交換，從它出發將引出極復雜的表達式。

如楊振寧在論文選集中所說：

這樣一來，我便陷入了困境，不得不罷手。然而，基本的動機仍然吸引著我，在隨后的幾年中我不時地再回到這個問題上來，但是每一次都困在同一個地方。當然， 于研究學問的人來說，一些看起來很好的想法，卻老是不成功，是每個人都會碰到的共同經驗。多數情況下，這種想法要不就只好放棄，要不就束之高閣。但是也有一些人堅持不懈，甚至執迷不悟。有時這種執迷不悟最后成為一樁好事。[按：楊先生寫這段話時也許曾想到 Einstein， 后者將狹義相對論推廣到廣義相對論，同樣花了七年之久。]

隨著越來越多的介子被發現以及各種各樣的相互作用的被考慮，我感覺迫切需要一種在寫出各種相互作用時大家都應遵循的原理。因此，在我再一次回到把規范不變性推廣出去的念頭上來。與我共用辦公室的Mills是哥倫比亞大學N. Kroll手下的研究生，即將取得博士學位。我們共同研究這個問題，最終寫成論文。

令楊振寧和Mills峰回路轉的，是一個換位子

他們將場強F定義為

(其中i是虛數單位， g是耦合常數。) 于是天塹變通途。誠然，事后從微分幾何的觀點來看，場強的這個定義確實是自然的，但考慮到楊振寧和Mills當時并沒有微分幾何的背景， 寫出這個公式就不簡單了。

從以上場強公式出發，楊振寧和Mills引入Yang–Mills泛函，考慮其歐拉–拉格朗日方程，就得到Yang–Mills方程，它是著名的Maxwell方程的推廣。跟Maxwell方程所描述的光子一樣，Yang–Mills方程描述的規范玻色子的質量也是零。這個問題一度令楊振寧很頭疼，因為他和Mills傾向于相信，帶電的規范粒子必定有質量。楊振寧也因此遭到物理學家Pauli的詰難，后者堅持認為這一理論不可靠。當楊振寧在普林斯頓高等研究所講述他和Mills的工作時，Pauli毫不客氣地批評。事實上，Pauli曾有類似的想法，但因為質量問題沒有解決而放棄。

圖6：Pauli一向以批評人見長。以上是他的一句名言，有個知名的數學物理普及網站就叫 "Not Even Wrong" (http://www.math.columbia.edu/ woit/wordpress/). 就連Einstein，他也不客氣：“You know,what Einstein has just said isn't so stupid.”

Einstein和Weyl曾聯合推薦 Pauli 擔任高等研究所的第二任所長，但被Pauli拒絕。后來 J. R. Oppenheimer (1904–1967) 接任。Pauli在1946 年獲得Nobel物理學獎，Weyl借用另一位Nobel獎得主N. Bohr (1885–1962)的話來評價他：“Pauli for many years has been the conscience and criterion of truth for a large part of the community of theoretical physicists.” 可以想見，Pauli的批評當時給楊振寧形成了巨大的心理壓力。

然而，楊振寧并未退縮，他寫道：“我們究竟應不應該發表這篇關于規范場的文章？在我們心中，這從來就不是一個真正的問題。我們的想法是美妙的，應該發表出來。”

2021年9月，為慶祝楊振寧先生百歲華誕，清華大學、中國物理學會、香港中文大學聯合主辦的楊振寧先生學術思想研討會的會徽，就嵌著Yang–Mill場強公式：

這個公式的重要性在1954年尚未認識到，20多年以后，才被充分認。我們將在第5節講述。

插話：Weyl

楊先生晚年論及規范場時，常常提及兩個人，一個是 Pauli，另一個是規范原理的創始人Hermann Weyl (1885–1955)，后者是普林斯頓高等研究所元老級別的數學教授。Weyl生前一直心心念要將規范不變原理加以推廣。遺憾的是，Weyl 去世前并未了解楊振寧和Mills的工作。可以料想，倘若Weyl有機會了解這一工作，那么規范場論可能在上世紀50年代就蓬勃發展了，當然很可能楊振寧本人的工作也會以規范場為主線貫穿。順便指出，楊振寧被視為Weyl在20世紀下半葉的衣缽傳人，在1985年Weyl誕辰百周年之際，楊振寧在蘇黎世做了“Hermann Weyl對物理學的貢獻”的精彩演講。

圖7：普林斯頓高等研究所的徽章，主題“真與美“。英國詩人濟慈有名句：”美者真，真者美。”

普林斯頓高等研究所的徽章主題“真與美”，恰好反映了Pauli與楊振寧的不同價值觀。Pauli選擇真；楊振寧選擇美。Weyl呢？他有一句經Dyson轉述的名言：“我的工作就是努力把真與美統一起來；當我不得不作出抉擇時，我常常選擇美。”

Weyl，1918年提出規范原理，試圖統一電磁場和引力場，但因為不符合物理常識遭到Einstein的反對。量子力學出現以后，規范原理得到復活，但令Weyl意外的是，它并未統一電磁場和引力場，而是統一了電磁場和量子力學中的電子-波場。Weyl為統一場論做了許多嘗試，直到1950年他都發表過這方面的文章。但在《半個世紀的數學》[8]一文中，他對此總結道：

人們試圖用這些幾何結構來描述引力場之外的自然界存在的其它物理場，像電磁場、電子-波場以及對應于其他幾種粒子的場。但是，在我看來，迄今為止所有力圖建立統一場理論的設想都失敗了。我們有極為合理的理由來用微分幾何的基本概念來解釋引力。但是，試圖把所有物理實體都“幾何化”或許是靠不住的。

三

反對稱張量的乘積不等式[1962-1963]

1962年，楊振寧發表了一篇關于凝聚態物理的文章，其中包含了一些純數學的結果。1963年，他又做了進一步發展。這些問題本身是饒有趣味的，但由于他采用的是物理學家的語言和記號 (約化密度矩陣)，以至于數學界鮮有人知。這里我們將他的工作翻譯成數學語言 (參見注釋[9]) 。

猜想 1 (楊振寧, 1963)設

，其中

是V上的

次外形式空間，

，則

在約束條件

下的最大值

為

這里

，而

。并且，最大值可在

取得，其中

此處θ1,…, θm是

的一組標準正交基。

楊先生本人在 1962 年證明了

之一等于1或2的情況。據筆者所知，目前整個猜想尚未解決。E.A. Carlen，E. H. Lieb，R. Reuvers在2016年的一篇文章中將ωr命名為Yang Pairing State (一個變體稱之為Sasaki–Coleman態，見F. Sasaki Eigenvalues of fermion density matrices， Phys. Rev. 138B，1338 (1965)，而Coleman本人則命名為Antisymmetrized Geminal Powers(AGP)，見A. J. Coleman，Structure of Fermion Density Matrices. II. Antisymmetrized Geminal Powers J. Math. Phys. 6，1425(1965) )。楊振寧當初提出這些態，是受到1957年關于超導的BCS理論 (Bardeen–Cooper–Schrieffertheory) 的啟發，其中有一個關鍵成分是所謂的Cooper配對。

2004年，數學家T. Iwaniec，J. Kauhanen，A. Kravetz，C. Scott在其合作文章中考慮了略微一般的問題，但這些作者并不了解，他們差不多是重復了楊振寧40年前的工作；而他們對這個一般問題也未能做出合理的猜測 (實際上他們對一個簡單的情形猜錯了，他們在p.214猜測 ，這小于猜想1給出的數) 。

順便指出，楊振寧所考慮的是Fermions體系，而Bosons體系的相應問題已經為L. Onsager (1903– 1976) 和O. Penrose[10](1929–，他是2020年諾貝爾物理學獎得主R. Penrose的哥哥他們還有一個知名的棋手弟弟 Jonathan Penros Penrose (1933–)。Penrose 當時是 Onsager 的博士后) 所考慮。楊振寧正是受到他們工作的啟發而考慮Fermions體系以及同時包含Bosons與Fermions的體系。

從數學上講，Fermions體系的波函數用反對稱的多重線性函數——即外代數——表示， 而Bosons體系的波函數用全對稱的多重線性函數表示，而對稱代數同構于多項式代數。對于Bosons體系，楊振 寧得到的結果可如下表述：

定理2 (Yang–Beauzamy 不等式) 設P，Q是

中的齊次多項式，則有

其中

表示Bombieri范數。

楊振寧在1962年的論文中就得到了這個結果，后來又被數學家B. Beauzamy在1990年得到。

四

Yang-Baxter方程[1967]

1963年，數學家E. Lieb與W. Liniger利用著名的Bethe擬設求解了一維玻色子在互斥作用下的本征值問題，1964年，物理學家J. B. McGuire也獨立解決了同一問題。1965年，McGuire考慮了費米子的類似問題，得到特殊情況下的部分結果，1967年Lieb和M. Flicker做了進一步推廣，但未完全解決。1967年，楊振寧和M. Gaudin（1931–）各自獨立地解決了一般問題。楊振寧通過利用一個推廣的Bethe擬設完成了這一工作，其文章極短，而Gaudin的全文是其博士論文。

楊振寧之所以對這個問題感興趣，是因為早年他就注意到Bethe擬設的妙處。Bethe擬設由物理學家H. Bethe (1906–2005) 在1931年提出，它大致說，若一個系統的哈密頓量具有某種對稱性，那么它具有某種特定形式的本征值和本征函數。

圖 8: 楊振寧與 Baxter

楊振寧的第一個研究生（B. Sutherland）的工作，充分利用了Bethe擬設的有效性,并在個別情形嚴格證明了其正確性 (Bethe擬設的數學內涵，1982年由數學家E. Gutkin在Integrable systems with delta-potential一文中揭示。)

在求解費米子的本征值問題時，楊振寧注意到，有一組等式很關鍵，確保了方程組的相容性 (系統的可積性)。這組等式1971年又被R. J. Baxter (1940–) 重新發現，從而被冠名為Yang–Baxter方程。

通過明確寫出Yang–Baxter方程的具體形式來理解它，對筆者和讀者來說都是極困難的.這里我們滿足于給出一個不失其精髓的簡化版本。從精神上講，Yang–Baxter方程有似于三個元素的全置換群S3的生成元之間的基本關系。如下圖所示：

圖9：從第一行第一個圖到第二個經歷的是σ1=(1, 2)，從第二個圖到第三個圖經歷的是σ2=(2, 3) ，之后的四步是重復兩次這些操作。最終的結果： (σ1σ2)3=1，即六步恰好回復原位。

Yang–Baxter方程與可積系統的發展，被俄羅斯L. Faddeev (1934–2017) 學派發揚光大。特別地，最初被用來描述Yang–Baxter方程的解的一個工具后來被V. Drinfeld定義為Yangian。

值得一提的是，2010年，楊振寧在與尤亦莊合作的文章中更正了1967年文章中末尾的一處錯誤，為這個問題畫上了圓滿的句號。

順便指出，2009–2010年間，楊振寧發表了7篇學術論文(均發表在Chinese Physics Letters) ，其中有5篇是與馬中騏教授合作。馬中騏教授告訴我，他們的工作產生了一些未解決的猜想：

楊先生和我合作的工作，用Thomas–Fermi方法計算電子密度分布的精確解。我們相信這是精確解，用了一些輔證，但不是嚴格證明。我們不會證也沒有精力去嚴格證明了。

南開大學陳省身數學研究所的葛墨林院士在一篇文章[11]特別分享了楊先生做物理的與眾不同:

物理從某種意義上是一種直覺。我有時問楊振寧先生，您怎么寫一篇文章就是經典文章？我問他怎么去推導？他說不對，我做這個之前，我早就知道是這個結果，先猜的。好物理都是先猜出來的。也就是說，他的物理圖像非常清楚，早就知道該做什么，然后去推。

這不由得令我們想起數學家E. Artin (1898–1962) 的一句名言；“我們的困難不在于證明，而在于學習要證明的是什么。”

五

Wu-Yang字典[1975]

1968–1969年，楊振寧在石溪講授一門廣義相對論的課程。有一天，他在黑板上抄下著名的Riemann曲率公式：

他突然發現這個公式跟他與Mills1954年文章中的場強公式非常相似。下課后他比較了這兩個公式，很快發現這兩個公式本質上是同一個。于是他就去求教數學系的系主任J. Simons. Simons告訴他，這兩個方程都是纖維叢理論中的曲率方程。后來，楊振寧就請Simons給物理系的同仁講拓撲學和纖維叢理論。楊振寧由此第一次了解到，規范場論的數學原來已經被數學家在優美的纖維叢理論中發展了。至此，楊振寧充分理解了規范場論的幾何涵義。例如，他跟Mills1954年猜出的場強公式恰好對應著曲率公式

，其中ω是聯絡形式， Ω是曲率形式，而d是外微分。如陳省身先生所說，“物理的力是一個曲率，數學家講曲率和物理學家講力其實是同一個觀念。”

楊振寧與Simons的交流，不由令人想到A. Einstein（1879–1955）與數學家M. Grossmann (1878–1936) 的故事。正是Grossmann向Einstein指出了Riemann幾何對于發展廣義相對論的重要性。據說，當年Einstein向老同學求教時，是這樣說的：“Grossmann，你一定要幫幫我，不然我會瘋掉！”也正是Simons讓楊振寧認識到纖維叢對于規范場論的重要性。

1975年，楊振寧與吳大竣合作，給出了規范場的整體表述，并給出了著名的Wu–Yang字典，在規范場和纖維叢之間架起了橋梁，從而用纖維叢的數學澄清了規范場中一些含混不清的概念。

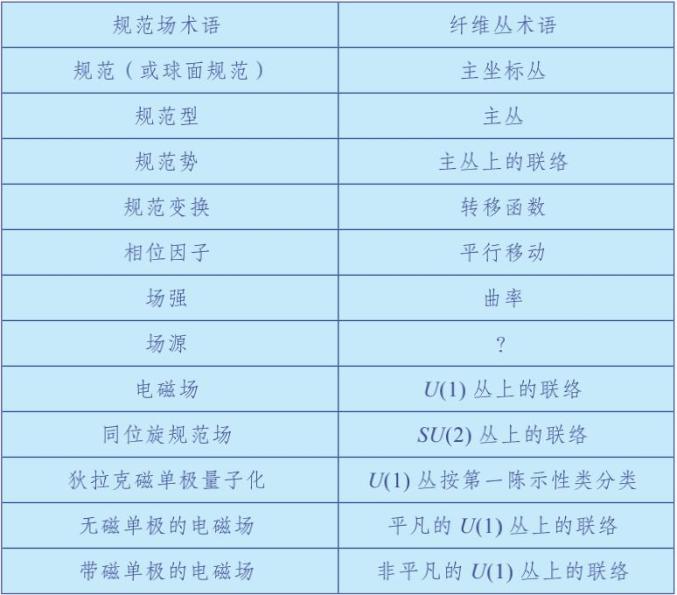
特別值得指出的，是楊振寧與吳大竣確立了，相位因子 (而不是場強) 才是規范場的恰當描述。從數學上，相當于說，在纖維叢的幾何中，聯絡 (而不是曲率) 才是首要的研究對象。順便指出，纖維叢上的聯絡之定義，是由法國數學家C. Ehresmann (1905–1979) 在1950年給出。Ehresmann是E. Cartan (1869–1951) 的學生，是陳省身的師兄，也是嚴志達 (1917–1999) 和吳文俊 (1919–2017) 的博士導師。

圖10：吳大竣與楊振寧，1982年攝于荷蘭萊登

楊振寧承認，規范場與纖維叢之間的緊密關系，已經多多少少被許多不同的作者(包括E。Lubkin，D. Finkelstein，J. M. Schiminovich，D. Speiser，J. A. Wheeler，B. S. DeWitt，A. Lichnerowicz，C. W. Misner，A. Trautman，H. G. Loos)在1960–1970年代察覺。但正如英國數學家、哲學家A. N. Whitehead (1861–1947) 在一篇題為The Organisation of Thought的演說中所說的：

在其關于形式的理論中，Aristotle和后繼的邏輯學家都非常接近邏輯變量的理論[11]。但科學的歷史告訴我們，非常接近真理跟真正懂得它的意義，是兩碼事。每一個重要的理論都被它的發現者之外的人說過。

楊振寧曾多次說，只是在與吳大竣寫完這篇文章以后，才終于欣賞到數學與物理 (即纖維叢與規范場) 之間謎一樣深刻與美妙的關系。當弄明白規范場就是纖維叢的聯絡以后，楊振寧就帶著吳大竣驅車前往伯克利，拜訪幾何學家陳省身。楊振寧曾回憶起這次拜訪：

40年代初，當他[陳省身]是中國昆明西南聯大的年輕教授而我是該校的學生時，我曾聽過他的課。那時，纖維叢在微分幾何里還未顯出重要性。陳教授也還未以他對Gauss–Bonnet定理的推廣及建立Chern類所做的貢獻而創造歷史。我們談了許多：朋友、家人、中國。當我們的談話轉移到纖維叢理論時，我告訴他，我終于從Simons那里學到了纖維叢理論和意義深遠的Chern–Weil定理之美妙。我說，規范場恰好是纖維叢上的聯絡，而后者是數學家在不涉及物理世界的情況下發展起來的，這實在令人驚異。我還加了一句：“這既令人震驚，也令人疑惑不解，因為你們數學家憑空夢想出了這些概念。”他馬上提出異議：“不，不，這些概念不是夢想出來的。它們是自然的，也是實在的。”

圖11：畫家范曾為陳省身和楊振寧創作的巨畫，作品懸掛于南開大學陳省身數學所

幾年前，我曾通過郵件訪談楊先生幾個問題，其中一個問題是：“您一生中最激動的時刻”是什么時候。他做如下答復：

我想我一生中靈魂最受震撼的時刻是：

a)在《鄧稼先》一文中描述的1971年的事情(收入《曙光集》，見“民族感情？友情”一節)[13]：

b)當我最終理解了，電磁學的數學恰好是數學家發展的優美的纖維叢理論(見我最近的文章《麥克斯韋方程和規范理論的觀念起源》中關于Maxwell和他向上帝禱告的評論[14]。

插話：楊振寧對華羅庚與陳省身的比較

楊振寧寫過多篇關于陳省身的文章，比如數學界耳熟能詳的佳句“千古寸心事，歐高黎嘉陳”就出自楊先生1973年的詩《贊陳氏級》。1991年，陳省身80大壽時，楊振寧寫了一篇文章《陳省身先生與我》。2013年，楊先生將這篇文章收錄《論文選集續集》[2]時，專門加了一個評論，比較了華羅庚與陳省身，很有意思，我們分享如次 (上書p.188) ：

伯林 (Isaiah Berlin，1900-1997) 普及了希臘關于哲學家的兩種不同類型的觀念：“狐貍掌握多門技藝，而刺猬則精通一門絕技。”我想這是一種極好的方式來描述華羅庚與陳省身的不同：華羅庚興趣廣泛，對數學的幾個不同分支做出了重要貢獻；而陳省身則專注于微分幾何一個分支，但他革新了這個分支，并且這個革新后來對20世紀的幾何、代數、分析、拓撲各個主要分支都有深遠的影響，甚至深入影響了近40年來理論物理學的發展。

2011年，楊振寧在南開大學舉辦的“陳省身先生100周年誕辰紀念會議”上宣讀了文章《菩薩、量子數與陳氏級》，介紹了數學家A. Weil (1906–1998) 1948年關于物理中的粒子可能與幾何拓撲中出現的一些分類現象有關的猜想，最終引出結語：如果Weil的猜想是對的，那么陳省身開創的示性類就要旁及物理世界最基本的結構了，那時“數學仙山的大雄寶殿中豈能不迎來一尊新菩薩[陳省身]”？

實際上，早在1979年，楊振寧就專門翻譯過Weil的一篇介紹陳省身的文章《我的朋友——幾何學家陳省身》，發表于《自然雜志》[15]。

順便說一句，楊先生非常關心近代中國的數學史研究，在他指導我完成關于Dyson的傳記以后，曾建議我考慮許寶騄(1910–1970)、閔嗣鶴 (1913–1973)、鐘開萊 (1917–2009) 和王浩 (1921–1995)。他曾告訴我，從氣質上講，在許、華、陳三位中，他最接近許。2019年，97歲的楊先生在《數學文化》發表的文章《許寶騄和“移棋相間法”》就源于他對許先生的關注。此外，2015年《紐約客》關于張益唐的報道[16]，也是楊先生第一時間建議我翻譯的 (見對美的追求：張益唐破解了純數學的一個神秘) 。

六

Dirac磁單極[1976-1978]

Dyson 在 2008 年 Einstein 公眾演講《》（點擊標題閱讀）中說，楊振寧在規范場論方面的這兩篇工作是“飛鳥”級別的[17]：

Weyl離開普林斯頓后不久，楊振寧從芝加哥來到普林斯頓，并住進了Weyl的舊居。在我這一代的物理學家中，楊作為一只領頭的飛鳥接替了Weyl的位置。當Weyl還在世的時候，楊和Mills發現了非阿貝爾規范場的Yang–Mills理論，這是對Weyl早期規范場思想的絕妙推廣。

……對稱決定相互作用這個思想，是楊振寧對Weyl思想的推廣。Weyl曾注意到規范不變性與物理守恒定律密切相關，但他未能更進一步，因為他只知道Abel規范場的規范不變性。然而，楊振寧通過引入非Abel規范場而使這種聯系更加緊密。由于非Abel規范場伴隨非平凡的李代數，場之間的相互作用的可能形式成為了唯一的形式，因此對稱決定了相互作用。這個觀點是楊振寧對于物理學最偉大的貢獻。這個貢獻是一只飛鳥的貢獻，她高高翱翔在小問題的雨林之上，而我們大多數人在雨林中耗盡我們的一生。

圖12：多年以后，Simons夫婦為清華大學高等研究院捐資建造招待訪問學者的寓所陳賽蒙斯樓

相形之下，楊振寧在規范場論的其它工作就沒那么石破天驚了，但有一個工作是特別令他自豪的。這個工作，是厘清并發展了Dirac的磁單極。最初也受到Simons的啟迪。正如楊振寧在論文選集中所說的：

研究場論的物理學家必須學習纖維叢的數學概念，這一點越來越清楚了。1975年初，我邀請Jim Simons給我和同事們做一系列的午餐演講，講授微分形式和纖維叢。他友好地接受了邀請。于是我們學到了Stokes定理，de Rham定理等等。我們所學的使得我們理解了Aharonov–Bohm實驗的數學涵義，以及Dirac的電荷與磁單極的量子化定律。吳大峻和我后來還弄懂了深奧而且非常普遍的Chern–Weil定理。

圖13：Weyl與楊振寧在普林斯頓的故居，Mercer Street 284號。曲徑通幽處，飛鳥相與還。

1931年，P. A. M. Dirac (1902–1984) 在一篇極其著名的文章中證明了，如果存在磁單極，那么磁荷g與電子的電荷e之間必定滿足關系 (其中h是Planck常數，c光速) ：

這個量子化條件非常引人注目。但Dirac最初的推理非常晦澀。簡單說，他的推理中，必須要求電磁勢有“奇性”。這在數學上難以言說。后來，當楊振寧拿著Dirac的論文給Simons看時，Simons說：“Dirac已經領先陳省身十多年了。”言下之意，Dirac的磁單極量子化公式，其實可以放在纖維叢的拓撲觀點下考慮。大致這樣理解，左邊是曲率的積分，右邊的整數是纖維叢的歐拉數。在數學上，曲率與歐拉數之間的聯系由Gauss–Bonnet公式給出，因此Dirac量子化條件恰好是Gauss–Bonnet公式對磁單極所對應的纖維叢的具體應用。

今天從纖維叢的觀念來看，Dirac磁單極的觀念并不神秘。但在長達40年的時間里，人們對它缺乏理解，很大程度上，就是因為缺乏恰當的數學語言描述它。這里我們穿插一個故事。

現在以李群方面的工作著稱于世的Harish-Chandra (1923–1983) 早年是Dirac的學生，因為沒有Dirac那種對物理學的神秘的“第六感”，后來轉到了數學。在1948年轉行到數學之前，他寫了最后一篇物理文章，討論一個受到Dirac論文啟發 (也許就是Dirac本人所提出) 的問題：在Dirac磁單極的場中運動的電子，是否存在束縛態？由于問題沒有從數學上得到恰當表述，Harish‐Chandra得到了錯誤的結論——不存在。正如對Harish-Chandra卓有研究的數學家R. Langlands (1936–) 在論文《Dirac磁單極與誘導表示》中所指出的[18]：

關鍵點在于，波函數可以視為具有度量和由電磁勢定義的聯絡的線叢的截面。

事實上，1976–1977年，楊振寧與合作者 (吳大峻、A. S. Goldhaber，Y. Kazama等) 正是利用這個洞見而得到了存在束縛態的正確結論。這個故事讓我們想起陳省身先生多次強調的一個觀點，這也許正是楊先生所欣賞的數學家的價值觀：

楊振寧與吳大竣、杜東生進一步考慮了電子、磁單極和電磁場的二次量子化理論，但只取得部分成功。所謂“文章千古事，得失寸心知”，楊先生一直期待能夠用R. Feynman (1918–1988) 路徑積分將他們發現的那個經典作用量量子化。

圖14：Dirac，他與Einstein和Fermi并列為楊振寧學生時代的三位偶像

楊振寧還將Dirac的U(1)磁單極推廣到SU(2)磁單極。順便指出，楊振寧對SU(2)情有獨鐘，因為與它對應的代數是四元數，U(1)對應的代數是復數，它是實數域上唯一的非交換可除代數。(這是著名的Frobenius定理的推論。楊先生有一次在郵件中曾問我，是否能證明不存在三維的實可除代數，并在后來的郵件中分享了他的證明——只用到三次實系數多項式必定有實根。)

稍加觀察，我們可以注意到，楊振寧的工作中有兩點特別突出：

(1)費米化：將Boson系統改為Fermion系統；見第3，4節，

(2)四元數化：將U(1)群推廣為SU(2)群；見第2節以及本節上一段。

楊振寧在《我的學習與研究經歷》一文中曾經說：“把問題擴大往往是一個好的策略。”楊振寧曾對他最后一個博士翟薈說[19]：“你要是真正懂一件事情，就要能對它做出generalization。你能generalize這個事情，才說明你真的懂了。”

插話：規范場論空前繁榮

1976年，楊振寧和Simons分別將第5節所提到的規范場–纖維叢字典給到此訪問的幾何學家I. Singer (1924–2021) 看，Singer看后非常激動，又分享給他在牛津的合作者M. Atiyah (1929–2019) ，進而在數學界引起熱烈反響。正是Singer將這個字典命名為“Wu–Yang字典”，并指出，字典中的“？”不是別的，正是Yang–Mills方程。J. Hadamard (1865–1963) 曾經說：“就廣義相對論來說，所有的數學家必須承認失敗。”對非Abel規范場論來說，數學家何嘗不是如此呢？要知道，這個推廣一直是Weyl晚年念念不忘的夢想！。

圖15：陳省身，他多次強調基本觀念的重要性。例如，在紀念Einstein誕辰100周年的演講中，他說到：“叢和聯絡這兩個幾何概念是非常簡潔的，我相信 Einstein 會喜歡它們。”

自數學家介入規范場論以后，規范場的發展得到空前繁榮。如果說1954年Yang–Mills開創歷史還只是“山有小口，仿佛若有光”的話，那么到1975年Wu–Yang字典出現以后，已經是“豁然開朗”的氣象了。回看歷史，在數學界，有一些主要人物 (“英雄造時勢”) 促成了規范場、同時也是幾何學的空前繁榮：Atiyah，Singer和陳省身之外，還有R. Bott (1923–2005)，N. J. Hitchin，R. S. Ward，S. K. Donaldson，E. Witten，A. Jaffe，Faddeev，Drinfeld，Yu. I. Manin，C. Taubes，K. K. Uhlenbeck，丘成桐等。正所謂“江山如此多嬌，引無數英雄競折腰”，恕我們這里不能一一展開。我們這里僅僅指出，Atiyah的論文集第五卷之標題就是“規范理論”，丘成桐也專門寫過一篇文章《規范場論與幾何》。

標志性的成果與事件有：1977年，Atiyah–Hitchin–Singer利用Atiyah–Singer的指標定理確定了自對偶Yang–Mills方程的解空間的維數；1978年，Atiyah和Jaffe在芬蘭首都赫爾辛基召開的國際數學家大會上分別了做了關于規范場的45分鐘報告；同年，Atiyah，Hitchin，Drinfeld和Yu. I. Manin給出了自對偶Yang–Mills方程的解空間的具體構造；1979年，加州伯克利大學為慶祝陳省身退休舉辦了為期一周的研討會(集結成著作《The Chern Symposium 1979》于次年出版)，Bott和楊振寧分別做了關于Yang–Mills方程和纖維叢與物理中的磁單極的報告；1979年，陳省身在《美國數學月刊》上撰文《從三角形到流形》(中譯文同年刊登于《自然雜志》)，專辟一節強調Yang–Mills規范場之重要性。

1979年恰逢Einstein誕辰100周年，世界各地都舉辦了紀念活動。在普林斯頓高等研究所，陳省身和楊振寧都參加了活動。陳省身做了題為“廣義相對論和微分幾何”的報告，再次強調了Yang–Mills規范場論。楊振寧則參與Bethe主持的題為“Einstein and the Physics of the Future”的小組討論（中譯文收入）。楊振寧提到，正是Einstein首先使用了“對稱支配相互作用”這一原則。后來，楊先生也說，他在科學上的最大成就可以用這句話概括：對稱支配相互作用。楊振寧還參加了在意大利里雅斯特為紀念Einstein誕辰100周年而召開的第二屆Grossmann會議，并做報告《Einstein和20世紀后半期的物理學》，其中他畫了一個二葉圖來比喻數學與物理的關系，并說道：

它們有各自的目標和截然不同的價值觀與傳統，在基礎概念的層面，它們令人驚訝地共享著某些概念，但即使如此，每個學科仍舊按著自身的脈絡生長著。

規范場的故事遠遠沒有結束。2000年，Clay數學所提出了21世紀的七個懸賞百萬的數學難題，其中最年輕的一個，就是Yang–Mills規范理論的質量間隙問題。

結語

從本文所介紹的幾項成就來看，楊先生的這些工作，凸顯了數學與物理之間的和諧與美妙。正如Dyson在1999年楊振寧退休研討會上的演講《一個保守的革命者》一文中所精辟總結的[19]：

楊振寧對數學美的品味在他的全部工作中熠熠生輝。它將他次要的計算轉化為袖珍的藝術品,將他更深刻的猜測轉化為杰作。它使得楊，一如它曾使得Einstein和Dirac，比其他人對自然的神秘運作看得更遠。

2014 年，在丘成桐65歲生日的慶祝活動上，楊振寧曾說:

有人問我，現在我重新選擇專業的話，我會做什么選擇？我現在看理論物理，發展很是緩慢，不像我們那個時代，所以我說我會選擇數學。

那么他會不會選擇像Yang–Mills質量間隙這樣的難題研究呢？我猜他更可能會遵循他在芝加哥大學的老師E. Fermi (1901–1956) 的教導：

那么楊先生可能會選擇哪些數學呢？我想，從歷屆邵逸夫數學獎得主的名單中可以得到線索。為什么呢，邵逸夫獎的設立與評選，楊先生都功不可沒。

縱觀楊先生這幾篇簡潔凝練的代表作，可以發現，楊先生對數學的美有極高的品味，對物理的真有極深的洞察，對歷史有敏銳通透的反思。不禁令人想起韓愈的名句 ：“李杜文章在，光焰萬丈長。”韓愈在下文中還慨嘆自己未能與李白杜甫生活在同一個時代 ：“伊我生其后，舉頸遙相望。夜夢多見之，晝思反微茫。”比起韓愈，我們是何其幸運 ：人與文同在，春風拂面來！

致謝

本文以作者2021年10月17日在“第十屆全國數學文化論壇學術會議”上的同名報告為底稿，在《數學文化》主編湯濤院士的建議下擴充完成。感謝嚴加安院士、湯濤院士對作者一如既往的鼓勵支持!感謝清華大學高等研究院許晨老師提供楊先生的諸多照片。感謝天津大學物理系戴伍圣老師和劉云朋老師、上海交通大學數學系的吳耀琨老師、重慶大學數學學院邵紅亮老師、中央民族大學理學院王兢老師、北京朝陽教研中心張浩老師、香港科技大學陳帥博士對初稿提出寶貴意見。感謝西北農林科技大學資環學院劉洋同學幫忙制作圖片。

后記

寫作本文，讓我想起華東師范大學數學系的張奠宙老師 (1933–2018)。十幾年前當我還是本科生的時候，正是通過閱讀他編纂的《楊振寧文集》而開始走近楊先生。20年前，張老師對楊先生做過一個極為精彩的訪談（參見《》），值得有興趣的讀者了解。

我還想到上海交通大學數學系的吳耀琨老師。2016年，他就邀請我做關于Lee–Yang單位圓定理的報告。然而，只是在這兩天準備這篇文章時我才領會到，原來單位圓定理如此漂亮。毫無疑問，正如丘成桐先生所說的：“楊振寧教授的工作中還有許多有待數學家發掘的寶藏，比如李政道–楊振寧關于多項式零點的單位圓定理。”最后，為滿足讀者的求知欲與好奇心，我再借花獻佛分享一條尋寶線索。

圖16：楊振寧先生90歲時，清華大學贈送給他的立方體。頂面刻著楊先生最喜愛的詩句“文章千古事，得失寸心知。”四個側面分別是楊先生在統計力學、規范場論、凝聚態物理和粒子物理方面的13項代表性成就。本文第1，4節屬于統計力學，第2，5，6屬于規范場論，第3節屬于凝聚態物理。對楊先生工作更專業的介紹，可見葛墨林院士的文章。

注釋

[1] 1922-2002，其父是中國著名數學家熊慶來（1893-1969）。

[2] 楊振寧：我對亞洲發展是一個樂觀的看法 ,《知識通訊評論》79 期 , 2009.05.01.

[3] 林開亮，戴森傳奇，《數學文化》第六卷 (2015 年 ) 第三期。

[4] 指普林斯頓高等研究所。

[5] 楊振寧，翁帆，《晨曦集》( 增訂版 )，商務印書館，2021. 254 頁。

[6] 季理真、林開亮，《楊振寧的科學世界：數學與物理的交融》，高等教育出版社，2018 年. 47頁

[7] 林開亮、鄭豪，從費爾馬多邊形數猜想到華羅庚的漸近華林數猜想——紀念楊武之先生誕辰 120 周年， 《數學文化》第七卷 (2016 年 ) 第二期。

[8] Hermann Weyl, A half-Century of Mathematics, American Math Monthly, 1951, 58(8): 523-553.

[9] 林開亮 , 楊振寧的一個猜想 ,《數學傳播》, 第 37 卷第 2 期 (2013 年 ) , 38-48. 去年華東師范大學出版的《百年科學往事——楊振寧訪談錄》 中，楊先生還專門提到這個問題。

[10] 他是 2020 年諾貝爾物理學獎得主 Roger Penrose 的哥哥 , 他們還有一個知名的棋手弟弟Jonathan Penrose (1933-).

[11] 葛墨林 , 物理教學的思考 , 《大學物理》第 32 卷 (2013 年 ) 第 9 期 .

[12] 這是他與羅素一起做出的發現 .

[13] 楊先生在文章中寫道：“1971 年 8 月 16 日，在我離開上海經巴黎回美國的前夕，……有人送了一封信給我，是稼先寫的，說他已經證實了，中國原子武器工程中除了最早于 1959 年底以前曾得到過蘇聯的極少‘援助’外，沒有任何外國人參加。此封短短的信給了我極大的感情震蕩。”

[14] 楊先生在文章中寫道：“麥克斯韋是個虔誠的教徒 . 我想知道 , 在做出如此巨大的發現后 , 麥克斯韋是否曾在禱告的時候因為揭示造物主的最大秘密之一而請求寬恕。 ”

[15] 安德烈·韋伊，楊振寧譯，我的朋友——幾何學家陳省身，《自然雜志》第2卷(1979年) 第8期。

[16] 對美的追求：張益唐破解了純數學的一個神秘。

[17] Freeman Dyson, Birds and Frogs, Notices of the AMS, 2008, 56 (2) : 212-223.

[18] Robert Langlands, The Dirac monopole and induced representations. Pacific Journal of Mathematics, 1986, 126(1): 145-151.

[19] 翟薈，楊先生研究風格對我的影響，收入《楊振寧先生百歲華誕文集》，將出版。

本文原載《數學文化》2022年第2期，感謝《數學文化》授權轉載。

原文鏈接：

原標題：《楊振寧六大數理工作賞析》

閱讀原文