撰稿 | 左 超   錢佳銘

2016年3月，谷歌旗下人工智能（AI）公司DeepMind憑借其開發的AlphaGo人工智能系統以總比分4:1戰勝圍棋世界冠軍李世石，引發了全人類對新一輪人工智能浪潮——深度學習技術的廣泛關注和持續熱議。從那刻起，人們見證了深度學習技術的快速崛起和廣泛應用——它以前所未有的性能解決了計算機視覺、計算成像和計算機輔助診斷等領域的諸多難題與挑戰。與此同時，Google、Facebook、微軟、蘋果和亞馬遜這五大科技巨頭無一例外投入越來越多資源搶占人工智能市場，甚至整體轉型為人工智能驅動的公司。它們開始“點燃”數據挖掘的“藝術”，并開發出易于使用的開源深度學習框架。這些深度學習框架使我們能夠使用預先構建和優化的組件集合，以更清晰、簡明和用戶友好的方式構建復雜、大規模的深度學習模型，而無需深入了解底層算法的細節。國內“BAT”也將深度學習技術作為重點戰略方向，憑借自身優勢積極布局人工智能領域。深度學習已經迅速地離開了學術界的殿堂并開始重塑工業界。

另一方面，光學計量學（Optical Metrology）是一類以光信號為標準/信息載體的測量科學和技術。它是一門古老的學科，因為物理學的發展從一開始就由光學計量技術所驅動的。但反過來，光學計量學也因激光、電荷耦合器件（CCD）和計算機的發明而發產生了重大變革。現如今已發展成為一個涵蓋廣泛的跨學科領域，并與光測力學、光學工程、計算機視覺和計算成像等學科緊密相關。鑒于深度學習在這些相關領域所取得的巨大成功，光學計量學的研究人員也無法抑制他們的好奇心，也開始積極投身到這一快速發展的新興領域中。不同于傳統的基于“物理先驗”方法，基于“數據驅動”的深度學習技術為解決光學計量領域的諸多挑戰性問題提供了新的可能，并展現出了巨大的應用潛力。

在此背景下，2022年3月，南京理工大學與新加坡南洋理工大學的研究團隊在國際頂級光學期刊《Light: Science & Applications》上聯合發表了題為"Deep learning in optical metrology: a review"的綜述文章，文章第一作者為南京理工大學左超教授，南京理工大學博士研究生錢佳銘為共同第一作者，南京理工大學左超、陳錢教授、新加坡南洋理工大學錢克矛教授為論文的共同通訊作者，南京理工大學為論文的第一單位。

文章系統總結了光學計量學中經典技術與圖像處理算法，簡述了深度學習的發展歷史、網絡結構及技術優勢，并對其在各種光學計量任務中（如條紋去噪、相位解調和相位展開）的具體應用進行了全面綜述。通過對比深度學習方法與傳統圖像處理算法的原理與思想上的異同，展示了深度學習在解決各種光學計量任務中“問題重構”和“實際性能”方面的獨特優勢。最后文章指出了深度學習技術在光學計量領域所面臨的挑戰，并展望了其未來潛在的發展方向。

傳統光學計量

圖像生成模型與圖像處理算法

光學計量技術將光的基本屬性（如振幅、相位、波長、方向、頻率、速度、偏振和相干性等）巧妙地用作被測物的信息載體，以實現對被測物的各種特征數據（如距離、位移、尺寸、形貌、粗糙度、應變和應力等）的獲取1。光學計量因其非接觸、高速、高靈敏度、高分辨率、高精度等優勢，在CAD /CAE、逆向工程、在線檢測、質量控制、醫療診斷、文物保護、人機交互等領域得到了日益廣泛的應用。在光學計量技術中，最常見信息載體為“條紋”與“散斑”。如大多數干涉測量法（經典干涉、光彈、數字散斑、數字全息等）所處理的圖像是由物光和參考光相干疊加而成的干涉條紋，被測物理量被調制于干涉條紋的相位信息中2??；此外，條紋圖案還可以非干涉的方式生成，如條紋投影輪廓術（FPP）直接投影結構光條紋圖案至被測物表面以測量物體的三維面型?。而在數字圖像相關（DIC）中，所拍攝的圖像則是樣品表面形變前后的散斑圖案，從中可獲得被測物全場位移和形變分布?；將DIC與立體視覺或攝影測量相結合，基于多視散斑圖像還可獲取被測場景的深度信息?。圖1總結了這些技術的圖像生成過程及其對應的數學模型。

圖1 傳統光學計量技術中的圖像生成過程及對應的數學模型

傳統光學計量離不開圖像處理技術，對條紋/散斑的圖像處理可以理解為由捕獲的原始強度圖像反演出所需的待測物理量的過程。通常情況下，該過程并非“一步到位”，而是由三個具有邏輯層次的圖像處理步驟所構成——預處理、分析和后處理。每個步驟都包含一系列圖像處理算法，這些算法層層疊加，形成一個“流水線”結構[圖2]，其中每個算法對應于一個“映射”運算，其將圖像/類似圖像的矩陣輸入轉化為相應維度（或重采樣的）的輸出。

（1）預處理：圖像預處理通過抑制或最小化不必要的干擾信號（如噪聲、混疊、畸變等）來提高圖像質量，光學計量中代表性的圖像預處理算法包括圖像去噪?、圖像增強1?、顏色通道分離11、圖像配準與校正12等。

（2）分析：圖像分析是圖像處理算法的核心步驟，用于從輸入圖像中提取與待測物理量相關的重要信息載體。在相位測量技術中，圖像分析的主要任務是從條紋圖像中重建相位信息，其基本算法包括相位解調13與相位展開1?；對于立體匹配技術，圖像分析是指確定散斑圖像（樣品表面形變前后的散斑圖案/多視散斑圖像）對應點間的位移向量，一般包括子集匹配和亞像素優化兩個步驟1?。

（3）后處理：圖像后處理的目的是進一步優化測量得到的相位數據或散斑位移場，并最終將它們轉化為待測物理量。光學計量中常見的后處理算法包括去噪1?、誤差補償1?、數字重聚焦1?、參量轉換1?等。圖3給出了光學計量圖像處理層次結構的概貌以及不同層中分布的各種圖像處理算法。

圖2 光學計量的典型圖像處理過程（如條紋投影輪廓術）可分為三個主要步驟：預處理（如去噪、圖像增強）、分析（如相位解調、相位展開）和后處理（如相位—深度映射）

圖3 光學計量圖像處理層次結構的概貌以及不同層中分布的各種圖像處理算法

深度學習技術

原理、發展與卷積神經網絡

深度學習是機器學習領域的一個重要分支，它通過構建模擬人腦信息處理神經結構的人工神經網絡（ANN），使機器能夠從大量歷史數據中進行自底向上的特征提取，從而實現對未來/未知樣本的智能決策。ANN起源于McCulloch和Pitts在1943年建立的生物神經元的簡化數學模型2?[圖4a]。1958年，Rosenblatt等21受生物神經元模型的啟發首次提出了可模擬人類感知能力的機器——單層感知機。如圖4b所示，單層感知機由單個神經元構成，神經元以偏置（b）和權重（w）為參數，通過非線性激活函數將輸入映射到輸出。感知器的提出激發了大量研究人員對ANN的興趣，對神經網絡的發展具有里程碑式意義。然而，單層感知器只能處理線性分類問題的局限致使隨后神經網絡的發展停滯了近20年。80 年代，反向傳播（BP）算法的提出使多層神經網絡的高效訓練成為了可能。其基于鏈式法則不斷調節神經元間的權值以減小多層網絡的輸出誤差，有效解決了非線性分類和學習的問題，引發了“淺層學習”的繁榮22。1989年，LeCun等23受哺乳動物視覺皮層結構啟發提出了卷積神經網絡（CNN）的思想，為現代計算機視覺與圖像處理奠定了深度學習的基礎。隨后隨著神經網絡層數的增加，BP算法的梯度消失/爆炸問題日益凸顯，致使90年代中期ANN的發展又陷入了停滯。2006年，Hinton等2?提出了一種深度置信網絡（DBN）的訓練方法來應對梯度消失問題；同時伴隨著計算機硬件性能、GPU加速技術的發展以及大量標記數據集的出現，神經網絡步入了第三次發展高潮，從“淺層學習”階段邁入了“深度學習”階段。2012年，基于CNN構架的AlexNet于ImageNet圖像識別比賽中一舉奪魁，使得沉寂20余年的CNN成為深度學習的主流框架之一2?。與此同時，一些新的深度學習網絡架構及訓練方法（如ReLU2?和Dropout2?）被提出以進一步解決梯度消失問題，促使了深度學習的爆炸式增長。2016 年，谷歌旗下AI公司DeepMind所開發的人工智能系統AlphaGo擊敗圍棋世界冠軍李世石，引發了全人類對深度學習技術的廣泛關注2?。圖4給出了人工神經網絡和深度學習技術的發展歷程與典型神經網絡的結構示意圖。

圖4 深度學習與人工神經網絡的發展歷程及典型神經網絡的結構示意圖

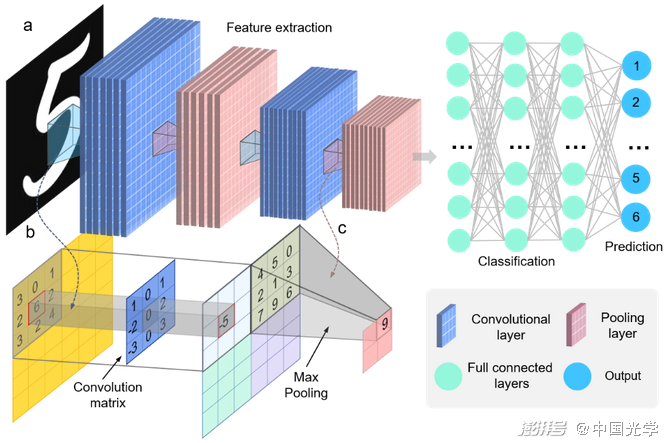
圖5 用于圖像分類任務的典型CNN結構  
a) 典型的CNN包括輸入層、卷積層、全連接層和輸出層  b) 卷積運算  c) 池化操作

上述單層感知機是最簡單的ANN結構，僅由單個神經元構成[圖4b]。深度神經網絡（DNN）由多層神經元相互連接而成，相鄰層間的神經元通常以全連接形式堆疊[圖4g]。在網絡訓練期間，神經元將相應的輸入乘以一個權重系數并與偏置值相加，通過非線性激活函數輸出至下一層，同時網絡損失被計算并反向傳播以更新網絡參數。不同于常規的全連接層，CNN使用卷積層對輸入數據進行特征提取2?[圖5a]。在每一層中，輸入圖像與一組卷積濾波器和添加的偏置進行卷積以生成一個新的輸出圖像[圖5b]。CNN中的池化層利用圖像的局部相關性原理對圖像進行子抽樣，在減少數據處理量的同時保留了有用信息[圖5c]。這些特征使得CNN廣泛應用于計算機視覺的任務中，如目標檢測3?和運動跟蹤31等。傳統的CNN構架大多面向“分類”任務，在輸出端舍棄了空間信息并產生了“向量”形式的輸出。然而，對于光學計量技術中的圖像處理任務，神經網絡必須能夠產生一個與輸入相同的（甚至更高）全分辨率輸出。為此應該使用沒有全連接層的全卷積網絡結構，這樣的網絡構架接受任意尺寸的輸入，用回歸損失進行訓練，并產生像素級的矩陣輸出。具有此類特征的網絡稱為“全卷積網絡結構”的CNN，其網絡架構主要包括以下三類：

（1）SRCNN：Dong等32跳過傳統CNN結構中的池化層，采用幾個卷積層簡單堆疊的方式在輸出端保留了輸入維度[圖6a]。利用該思想構建的SRCNN成為用于圖像超分辨任務的主流網絡框架之一。

（2）FCN：全卷積網絡（FCN）是由Long等提出的用于語義分割任務的網絡框架33。如圖6b所示，FCN使用傳統CNN[圖5]的卷積層作為網絡編碼模塊，將全連接層替換為反卷積層作為解碼模塊。反卷積層能夠對最后一個卷積層的特征圖進行上采樣使其恢復到與輸入圖像相同尺寸的輸出。此外，FCN通過跳級結構將粗糙的高層特征與細致的低層特征相結合，使網絡在保留像素級輸出的同時更好地恢復了細節信息。

（3）U-Net：Ronneberger等對FCN作出改進并提出U-Net網絡3?。如圖6c所示，U-Net的基本結構包括一個壓縮路徑和一個擴展路徑。壓縮路徑作為網絡的編碼器，使用四個卷積塊（每個卷積塊由三個卷積層和一個池化層構成）對輸入圖像進行降采樣并獲得壓縮特征表示；擴展路徑作為網絡解碼器使用轉置卷積的上采樣方法來輸出與輸入相同尺寸的預測結果。U-Net采用跳躍連接對壓縮路徑和擴展路徑進行特征融合，使得網絡可以在淺層特征和深層特征中自由選擇，對語義分割任務來說更有優勢。

上述全卷積網絡結構的CNN能夠將任意大小的輸入圖像轉化為像素級的矩陣輸出，這與光學計量任務中圖像處理算法所對應的“映射”運算的輸入輸出特征完全吻合，因此可以非常方便地對傳統圖像處理任務進行“深度學習替換”，這為深度學習在光學計量領域的快速崛起奠定了基石。

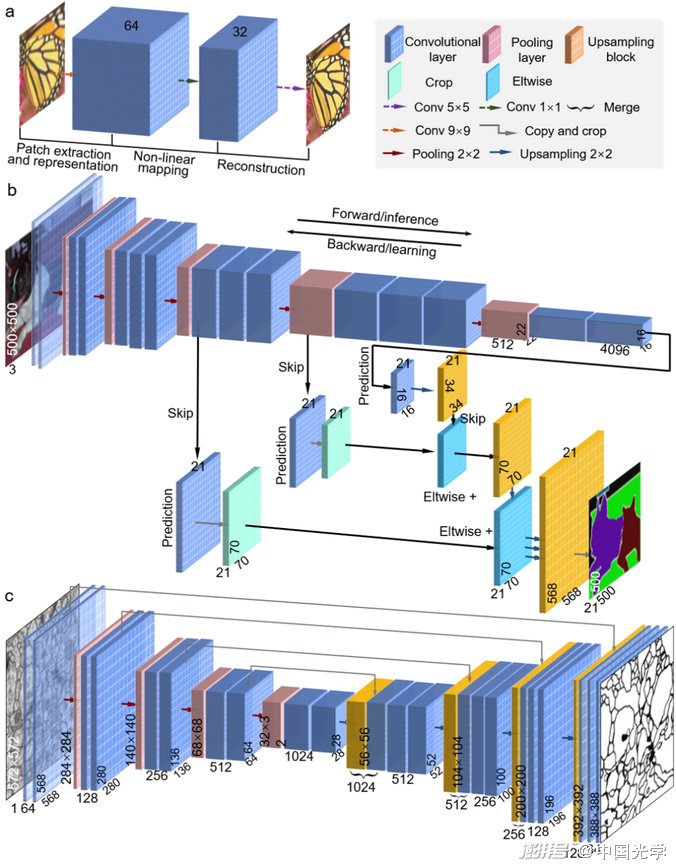
圖6 三種能夠產生像素級圖像輸出的用于圖像處理任務的代表性全卷積網絡結構的CNN
a) SRCNN   b) FCN   c) U-Net。

深度學習下的光學計量

思想與方法論的轉變

在光學計量技術中，原始條紋/散斑圖像與被測物理量間的映射可描述為從參數空間到圖像空間的正向物理模型和測量噪聲的組合，這可以解釋光學計量中幾乎所有原始圖像的生成過程。但從原始圖像中提取待測物理量是一個典型的“逆問題”。求解這樣的逆問題面臨著諸多挑戰，如：未知或不精確的正向物理模型、誤差累積和局部最優解以及逆問題的病態性等。在計算機視覺和計算成像領域，解決逆問題的經典方法是通過引入被測物的先驗作為正則化手段限定解空間以使其良態化[圖7]。而在光學計量領域，解決逆問題的思路則與之大相徑庭。根本原因在于光學計量通常是在一個“高度可控”的環境中進行的，因此更傾向于通過一系列“主動策略”，如照明調制、物體調控、多次曝光等來“主動調整”圖像的采集過程，這就可將原先的“病態逆問題”重塑為一個“良態且足夠穩定的回歸問題”。例如由單幅條紋圖像解調絕對相位：由于正向物理模型中缺乏足夠的信息可以用來唯一穩定地求解相應的逆問題，該逆問題是病態的。而對于光學計量的研究者來說，解決該問題的方法非常簡單：我們可以進行多次測量，通過獲取額外的多頻相移條紋圖像，絕對相位的獲取問題就演化為了一個良態的回歸問題。我們可以很容易地通過多步相移法13和時間相位展開法1?來從這些條紋圖像中恢復出被測物的絕對相位信息[圖8]。

圖7 在計算機視覺中（如圖像去模糊），由于從參數空間映射到圖像空間的正向物理模型不理想，所產生的逆問題是病態的。典型的解決方案是加入一些有助于正則化的先驗假設（平滑），將原始的病態問題重新表述為良態的優化問題

圖8 光學計量通過主動控制圖像采集過程，將病態的逆問題轉化為良態的回歸問題。如在條紋投影輪廓術中，通過獲取不同頻率的額外相移條紋圖像，絕對相位可以很容易地通過多頻相移法和時間相位展開法來獲取

然而當我們走出實驗室，進入現實世界的復雜環境時，情況就可能會大相徑庭。上述主動策略往往對測量條件和被測對象施加了嚴格限制，例如：穩定的測量系統、極小的環境干擾、靜止的剛性物體等。然而對于許多具有挑戰性的應用而言，如惡劣的操作環境與快速運動的物體等，可能使上述主動策略成為一種“奢侈”甚至是不切實際的要求。在這種情況下，傳統的光學計量方法將面臨嚴重的物理和技術限制，如有限的數據量和正向模型的不確定性。如何從最少的（最好是單幀）條紋圖案中提取高精度的絕對（無歧義）相位信息，仍然是當今光學計量學中最具挑戰性的問題之一。因此，我們期待著光學計量學原理和方法的創新和突破，這對其未來的發展具有重要意義。

深度學習作為近年來興起的一種“數據驅動”技術，在光學計量領域受到越來越多的關注，并在近幾年取得了豐碩的成果。不同于傳統物理模型驅動的方法，深度學習方法通過人為創建一組由真實目標參數和相應原始測量數據構成的訓練集，利用ANN建立了它們的映射關系，從訓練數據集中學習網絡參數以解決光學計量中的逆問題[圖9]。相比于傳統的光學計量技術，深度學習將主動策略從實際測量階段轉移到網絡訓練階段，從而獲得了以下三項前所未有的優勢：

1）從“模型驅動”到“數據驅動”：深度學習顛覆了傳統的“物理模型驅動”方式，并開啟了基于“數據驅動”的新范式。重建算法（逆映射）可以從實驗數據中學習，而不需要有關物理模型的先驗知識。若訓練數據集是在真實實驗環境下（包括測量系統、樣品類型、測量環境等）基于主動策略所采集的，且數據量充足（多樣性），那么訓練出來的模型應該能更精確、更全面地反映真實情況，因此通常會比傳統基于物理模型的方法得到更準確的重建結果。

（2）從“分步分治”到“端到端學習”：與傳統的獨立解決任務序列的傳統光學計量方法相比，深度學習允許“端到端”學習結構，其中神經網絡可以一步學習原始圖像數據與所需樣本參數之間的直接映射關系，如圖10所示。與“分步分治”方案相比，“端到端”學習方法具有協同作用的優點：它能夠在執行不同任務的網絡部分之間共享信息（特征），與獨立解決每個任務相比有助于獲得更好的整體性能。

（3）從“求解線性逆問題”到“直接學習偽逆映射”：深度學習利用復雜的神經網絡結構和非線性激活函數來提取樣本數據的高維特征，直接學習一個能夠充分描述整個測量過程（從原始圖像到待測物理量）的非線性偽逆映射模型（“重建算法”）。對于比傳統方法的正則化函數或指定先驗，深度學習所學習到的先驗信息是針對真實實驗數據的統計量身定制的，這原則上為求解反問題提供了更強、更合理的正則化。因此其繞過了求解非線性病態逆問題的障礙，可以直接建立輸入與期望輸出之間的偽逆映射關系。

圖9 基于深度學習的光學計量技術  
a) 在基于深度學習的光學計量技術中，通過構建一個深度神經網絡從數據集中學習圖像空間到參數空間的映射關系  b) 通過實驗或仿真獲得訓練數據集的過程。

圖10 深度學習與傳統算法在條紋投影領域的對比
a) 條紋投影輪廓術的基本原理是基于光學三角測量法的三維重建（左）。其步驟一般包括條紋投影、相位恢復、相位展開和相位-高度映射  b) 基于深度學習的條紋投影輪廓術是由大量訓練數據所驅動的，經訓練后的網絡模型可以直接從單幀條紋中預測出其中所編碼的深度信息

深度學習在光學計量學中的應用

圖像處理算法的全面革新

由于上述優點，深度學習在光學計量中受到越來越多的關注，為光學計量技術的概念帶來了顛覆性的變革。深度學習摒棄了對傳統“正向物理模型”和“逆向重構算法”的嚴格依賴，以“樣本數據驅動”的方式重塑了幾乎所有光學計量技術中數字圖像處理的基本任務，打破了傳統光學計量技術的功能/性能疆界，從極少的原始圖像數據中挖掘出更多場景的本質信息，顯著提升了信息獲取能力，為光學計量技術打開了一扇新的大門。圖11回顧了在光學計量領域采用深度學習技術的典型研究工作。下面按照傳統光學計量技術的圖像處理層次列舉深度學習在光學計量學中的具體應用案例。

圖11 光學計量中的深度學習：由于深度學習為光學計量技術從概念上所帶來了重大改變，光學計量學中幾乎所有任務的實現方式都被深度學習所革新

（1）圖像預處理：早期將深度學習應用于光學計量的工作集中于圖像預處理任務，如圖像去噪3?、圖像增強3?等。Yan等3?構建了一個由20個卷積層組成的CNN來實現條紋圖像去噪[圖12a]。由于無噪聲的理想條紋圖像很難通過實驗獲取，他們仿真了大量添加高斯噪聲的條紋圖像（網絡輸入）和相應的無噪聲數據（真值）用作神經網絡的訓練集。圖12d-圖12e給出傳統去噪方法——加窗傅里葉變換法（WFT3?）與深度學習方法的去噪結果。從結果中可見，基于深度學習的方法克服了傳統WFT的邊緣偽影，表現出更好的去噪性能。Shi等3?提出一種基于深度學習的條紋信息增強方法[圖13a]。他們將真實場景中捕獲的條紋圖像和相應的質量增強圖像（通過將兩幅相移量為π的條紋圖像相減獲取）用作數據集訓練神經網絡，以實現對條紋圖像到質量增強條紋信息之間的直接映射。圖13b-圖13d顯示了傳統傅里葉變換法（FT）3?和深度學習方法對運動的手的三維重建結果，從中可見深度學習方法在成像質量上明顯優于傳統方法。

圖12 基于深度學習的條紋圖像去噪方法及不同方法的去噪結果3?
a) 使用深度學習進行條紋去噪的流程：將帶有噪聲的條紋圖像作為神經網絡的輸入，直接預測去噪后的圖像  b) 輸入噪聲圖像  c) 真實相位分布  d) 深度學習的去噪結果  e) WFT3?的去噪結果

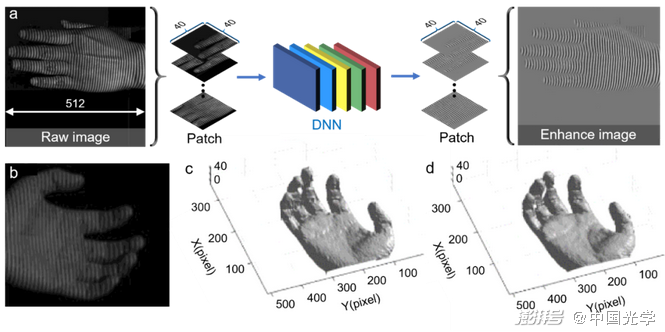
圖13 基于深度學習的條紋信息增強方法及不同方法下的三維重建結果3?
a) 使用深度學習進行條紋信息增加的流程：采集的原始條紋圖像和質量增強圖像被用來訓練DNN，以學習輸入條紋圖像到輸出質量增強條紋信息之間的映射  b) 輸入條紋圖像  c) 傳統FT法38的三維重建結果  d) 深度學習方法的三維重建結果

（2）圖像分析：圖像分析是光學計量技術中最核心的圖像處理環節，因此大多數應用于光學計量學的深度學習技術都是為了處理與圖像分析相關的任務。對于相位測量技術，深度學習在相位解調和相位解包裹方面得到了廣泛的探索。Zuo等3?首次將深度學習技術應用于條紋分析中，并有效提高了FPP的三維測量精度。該方法的思想在于僅采用一幅條紋圖像作為輸入，利用CNN來模擬傳統相移法1?的相位解調過程。如圖14a所示，構建兩個卷積神經網絡（CNN1和CNN 2），其中CNN 1負責從輸入條紋圖像（I）中提取背景信息（A）；隨后CNN 2利用提取的背景圖像和原始輸入圖像生成所需相位的正弦部分（M）與余弦部分（D）；最后，將該輸出的正余弦結果代入反正切函數計算得到最終的相位分布。相比于傳統單幀相位解調方法 (FT3?和WFT3?)，基于深度學習的方法能夠更為準確地提取相位信息，特別是針對具有豐富細節的物體表面，相位精度可提升50%以上，僅采用一幅輸入條紋圖像但總體測量效果接近于12步相移法[圖14b]。該技術目前已被成功應用于高速三維成像,實現了速度高達20000Hz的高精度三維面型測量??[圖14c]。Zuo等還進一步將深度學習從相位解調推廣至相位展開，提出一種用于單幀三維形貌測量的基于深度學習的幾何相位展開方法?1。如圖15a所示，多視幾何系統下捕獲的立體條紋圖像對及參考面信息被送入CNN中以確定條紋級次。圖15b-圖15e給出了傳統幾何相位展開方法?2???和深度學習方法獲得的三維重建結果。這些結果表明，基于深度學習的方法在僅投影單幀條紋圖像的前提下，可以在更大的測量體積內、更魯棒地實現對稠密條紋圖像的相位展開。

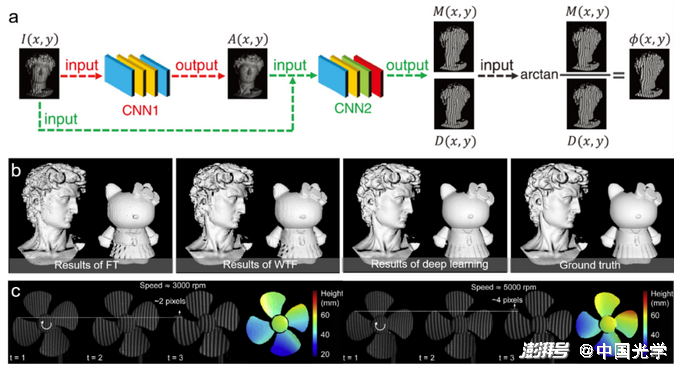
圖14基于深度學習的條紋分析方法及不同方法下的三維重建結果3?  a) 基于深度學習的條紋分析方法流程：首先通過CNN1從單幀條紋圖像I中預測出背景圖像A；然后采用CNN2實現條紋圖案I、背景圖像A與生成所需相位的正弦部分M和余弦部分D之間的映射；最后通過正切函數可以得到高精度包裹相位信息  b) 不同相位解調方法（FT3?、WFT3?、基于深度學習的方法和12步相移法13）的三維重建的比較   c) 使用深度學習方法對高速旋轉的臺扇的深度重建結果??

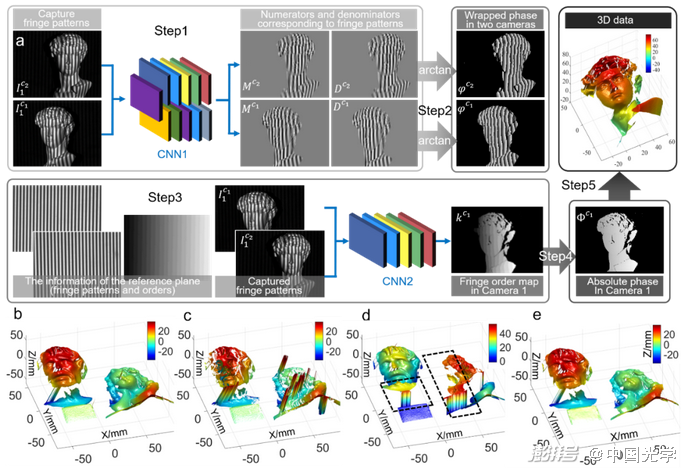
圖15基于深度學習的幾何相位展開方法及不同方法下的三維重建結果?1  a) 由深度學習輔助的幾何相位展開方法的流程：CNN1從立體條紋圖像對中預測包裹相位信息，CNN2從立體條紋圖像對及參考信息中預測條紋級次。通過預測的包裹相位和條紋級次可以恢復絕對相位，然后進行三維重建  b) 結合相移法13、三相機幾何相位展開技術?2和自適應深度約束法??獲取的三維重建結果  c)結合相移法13、雙相機幾何相位展開技術?2獲取的三維重建結果  d)基于參考面的幾何約束方法?3獲取的三維重建結果  e)深度學習方法獲取的三維重建結果

深度學習也被廣泛應用于立體匹配，并獲得比傳統子集匹配和亞像素優化方法更好的性能。Zbontar和LeCun??提出一種用于立體圖像視差估計的深度學習方法[圖16]。他們構建了一個暹羅型CNN，通過從兩個圖像塊中學習相似度量來解決匹配成本計算問題。CNN的輸出被用于初始化立體匹配成本，然后通過基于交叉的成本聚合和半全局匹配精煉初始成本進而實現視差圖估計。圖16d-圖16h是由傳統Census??變換法和深度學習方法獲取的視差圖像，從中可以看出，基于深度學習的方法實現了更低的錯誤率和更好的預測結果。Pang等??提出一種用于亞像素匹配的級聯CNN架構。如圖17a所示，首先通過帶有上采樣模塊的DispFulNet從輸入立體圖像對中預測初始視差估計，然后通過沙漏結構的DispResNet生成多尺度的殘余信號，綜合兩網絡輸出最終獲取亞像素精度的視差圖。圖17d-圖17g展示了由DispfulNet和DispResNet預測的視差圖及誤差分布情況。從實驗結果可以看出，經過第二階段DispResNet的優化，視差圖的質量得到了明顯的改善。

圖16  基于深度學習的子集匹配方法及不同方法的視差估計結果??  a) 使用深度學習進行視差圖估計的算法流程：暹羅型CNN被構建用于從兩個圖像塊中學習相似度量以解決匹配成本計算問題，并通過一系列后處理最終實現視差估計  b-c) 輸入的立體圖像  d) 真值  e, g) Census??和CNN獲取的視差估計結果

圖17  a) 基于深度學習的亞像素匹配方法：首先通過DispFulNet從輸入立體圖像對中預測初始視差估計，然后通過沙漏結構的DispResNet生成多尺度的殘余信號，綜合兩網絡輸出最終獲取亞像素精度的視差圖??  b) 輸入立體圖像的左視角  c) 真值  d-g) DispfulNet和DispResNet預測的視差圖及誤差分布情況

（3）后處理：深度學習在光學計量的后處理階段（相位去噪、誤差補償、數字重聚焦、相位-高度映射等）也發揮著重要作用。如圖18a所示，Montresor等??將噪聲相位圖像的正弦和余弦分量輸入CNN中以預測去除噪聲的高質量相位圖像，預測的相位被再次反饋到CNN中進行迭代提煉以達到更好的去噪效果。圖18b-圖18e給出了傳統WFT3?法和深度學習方法的相位去噪結果。實驗結果表明CNN能夠實現比WFT峰谷相位誤差更低的去噪性能。

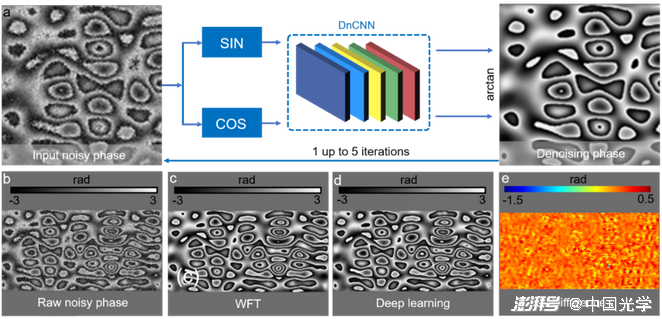
圖18  基于深度學習的相位去噪方法及不同方法的相位去噪結果??  a) 使用深度學習進行相位去噪的流程：噪聲相位圖像的正弦和余弦分量被輸入CNN以預測去除噪聲的高質量相位圖像，預測的相位被再次反饋到CNN中進行迭代提煉以達到更好的去噪效果  b) 輸入噪聲相位圖像  c) WTF3?的去噪結果  d) 深度學習的去噪結果  e) WTF與深度學習方法去噪結果的對比

Li等??提出了一種基于淺層BP神經網絡的用于條紋投影輪廓術的相位-高度映射方法。如圖19a所示，相機圖像坐標及對應的投影儀圖像水平坐標被用作網絡輸入以預測被測物的三維信息。為了獲取訓練數據，將圓點標定板固定于高精度位移臺并在不同的深度位置處捕獲標定板的條紋圖像。通過提取標定板圓點的亞像素中心，并利用絕對相位計算每個標記中心對應的相機和投影儀圖像的匹配點。圖19c和圖19d是由傳統相高轉換方法??和神經網絡方法獲取的階梯狀標準件三維面型結果的誤差分布情況，該結果表明基于神經網絡的方法可以從大量數據中學習出更加準確的相高模型。

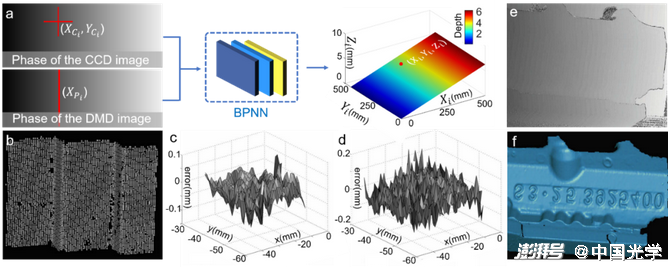
圖19  a) 基于學習的相位-深度映射方法：相機圖像坐標及對應的投影儀圖像的水平坐標被用作網絡輸入以預測被測物的三維信息??  b) 基于學習的方法獲取的階梯狀標準件的三維結果  c、d) 傳統相高轉換方法??和神經網絡方法獲取的階梯狀標準件三維面型結果的誤差分布情況  e、f) 復雜工件的輸入相位圖像及輸出三維信息

深度學習在光學計量領域面臨的挑戰與機遇

目前，深度學習已逐漸“滲透”進了計算成像與光學測量這一學科中，并在條紋分析、相位恢復、相位展開等方面展現出令人驚嘆的性能以及強大的應用潛力。然而，目前深度學習在光學計量領域仍然面臨諸多挑戰：

(1)   深度學習作為一種數據驅動的技術，其網絡輸出的性能很大程度上取決于大量標記的訓練數據。而大部分光學計量實驗的數據采集過程較為復雜耗時，且往往數據采集后無法獲取準確可靠的理想真值[圖20]。

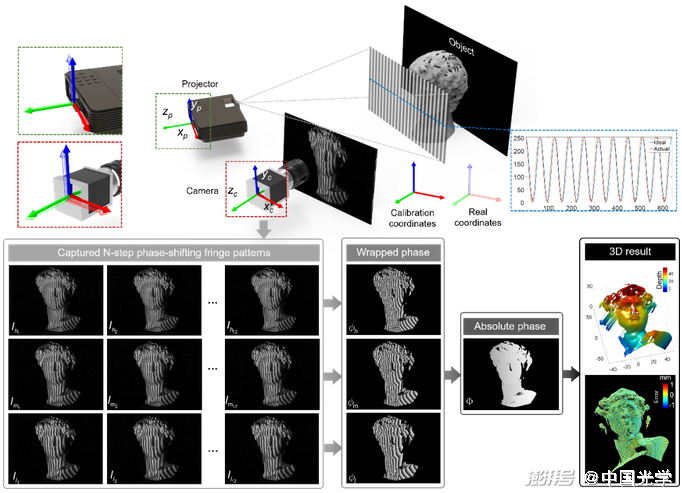
圖20  深度學習在光學計量中的挑戰-——獲取和標注訓練數據的高昂代價。以條紋投影輪廓術為例，采用多頻時間相位展開法以投影大量條紋圖像為代價獲取高質量訓練數據。然而在實際操作中，硬件誤差、環境光干擾、標定誤差等因素使得通過傳統的算法很難獲取理想真值

(2)   到目前為止，仍然沒有任何理論可以清楚地解釋針對特定的成像需求，到底選擇什么樣結構的神經網絡最為合適[圖21]？

(3)   深度學習的成功通常取決于從訓練樣本中學習和提取的“共同”特征作為先驗信息。因此，當人工神經網絡面對“罕見樣本”時，它極易給出一個錯誤的預測結果并且毫無察覺。

(4)   不同于傳統基于物理模型方法“透明式”推演過程，當前大多數基于深度學習方法的決策過程通常被認為是由訓練數據所驅動的“黑匣子”。而在光學計量中，可解釋性往往至關重要，因其確保了錯誤的可追溯性。

(5)   由于信息并不會"無中生有"，深度學習所獲得的結果不可能總是準確可靠的。這對于光學測量的許多應用領域而言往往是致命性的，如逆向工程、自動控制、缺陷檢測等。在這些場合，測量結果的準確性、可靠性、可重復性以及可回溯性是首要考慮的因素。

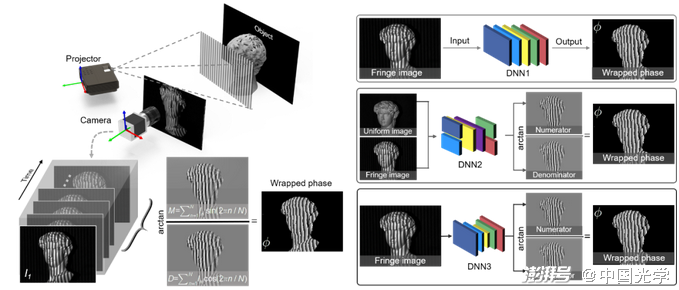
圖21  深度學習在光學計量中的挑戰——模型設計和算法選擇的經驗主義。以條紋投影輪廓術中的相位提取為例，同一任務可以由不同的神經網絡模型以不同的策略來實現：通過DNN1可以將條紋圖像直接映射到相應的相位圖；也可通過DNN2從條紋圖像和相應的背景圖像中輸出用于計算相位信息的正切函數的分子項和分母項；使用更強大的DNN，可直接從條紋圖像中預測分子和分母

盡管上述挑戰還沒有得到充分解決，隨著計算機科學與人工智能技術的進一步發展，可預計未來深度學習將通過以下三個方面在光學計量中發揮愈發突出的作用：

(1) 搭載深度學習技術發展的“順風車”，將其中的新興技術（如對抗學習、遷移學習、自動化機器學習等）運用到光學計量領域，可以促進深度學習在光學計量領域中的廣泛接受與認可。

(2) 將貝葉斯統計學與深度神經網絡相結合以對估計結果的不確定性進行估計與量化，基于此可以評估神經網絡何時產生不可靠的預測?1。這在“盲目信任”與“全盤否定”之間給了研究人員另一種可能的選擇，即“選擇性”采納。

(3) 描述圖像生成的先驗知識與物理模型和從實驗數據中學習的數據驅動模型二者間協同作用，能夠將光學計量領域的更多專業知識引入深度學習框架中，為解決特定的光學計量問題提供更多高效且“物理上合理”的解決方案[圖22]。

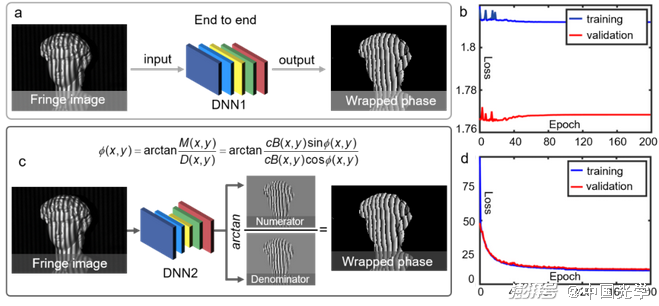
圖22  將物理模型引入深度學習可為特定光學計量問題提供更為“合乎情理”的解決方案。a) 基于端到端網絡結構（DNN1）從條紋圖像中直接預測包裹相位  b) 端到端策略很難精準復現2π相位截斷，導致網絡的損失函數訓練時無法收斂  c) 將傳統相移法的物理模型納入深度學習，從條紋圖像中預測用于計算相位信息的正切函數的分子項和分母項39  d) 結合物理模型的深度學習網絡的損失函數訓練時可穩定收斂

總結與展望

毋庸置疑，深度學習技術為解決光學計量領域的諸多挑戰性問題提供了性能強大且具有發展潛力的全新解決方案，并促進了光學計量學從“基于物理和知識的建模”向“基于數據驅動的學習”范式的轉變。大量已發表的文獻結果表明，針對特定問題通常基于深度學習的方法能夠提供優于傳統的基于知識或物理模型的方法的性能，特別是針對許多物理模型復雜且所能獲得的信息量有限的光學計量任務。

但不得不承認，目前深度學習技術在光學測量領域仍處于發展的早期階段。該領域中相當一部分研究人員是嚴謹且理性的，他們對現階段缺乏可解釋性的“黑匣子”式的深度學習解決方案是抱有質疑的，且對其在工業檢測和生物醫療等方面的應用是持觀望態度的。我們應該全盤接受深度學習作為我們解決問題“殺手锏”，還是拒絕這樣的“黑匣子”解決方案？這是當前光學計量界極具爭議的問題。

從正面來看，深度學習的出現為光學計量這一“傳統”領域帶來新的“生機”。它在光學計量領域的“全面滲透”也向我們展示了人工智能技術為光學計量領域帶來巨大的變革的可能性。反過來，我們也不該高估深度學習的力量，并把它當作解決光學計量未來發展所遇到的每個挑戰的“萬能鑰匙”。在具體實踐中，我們應理智地評估將深度學習用于特定任務所需的大量數據資源、計算資源和時間成本是否值得。特別是針對很多并不是那么“嚴苛”的應用場合，傳統基于物理模型與“主動策略”的技術能夠以更低的復雜度和更高的可解釋性獲得更好的結果時，我們勇于對深度學習說“不”！

在未來幾年內，深度學習是否會取代傳統技術在光學計量領域的角色，發揮顛覆性的作用？很明顯，沒有人可以預測未來，但我們可以參與其中。不管您是光學計量領域鐘情于傳統技術的“老司機”，還是在該領域涉足不久的“新手上路”，我們都鼓勵您能夠搭上這趟“順風車”—— 去大膽地嘗試一下深度學習吧！因為它真的很簡單，而且往往很奏效！

附注：本文附帶了一個深度學習用于單幀條紋分析的示例程序（Supplemental Material File #1）及其詳細的步驟指南（Supplementary Information），以方便讀者的學習與理解。更多本文相關的詳細內容，請點擊 https://www.nature.com/articles/s41377-022-00714-x 來閱讀全長54頁的論文正文。

論文信息

Zuo, C., Qian, J., Feng, S. et al. Deep learning in optical metrology: a review. Light Sci Appl 11, 39 (2022). 

https://doi.org/10.1038/s41377-022-00714-x

本文第一作者為南京理工大學左超教授，南京理工大學博士生錢佳銘為共一作者，合著者包括南京理工大學馮世杰副教授、南京理工大學博士生尹維、南京理工大學博士生李藝璇、英國倫敦瑪麗女王大學博士生樊鵬飛、南京理工大學韓靜副教授、新加坡南洋理工大學錢克矛教授、南京理工大學陳錢教授。

參考文獻

1.G?svik, K. J. Optical metrology. (John Wiley & Sons, 2003).

2.Creath, K. V phase-measurement interferometry techniques. in Progress in optics vol. 26 349–393 (Elsevier, 1988).

3.Aben, H. & Guillemet, C. Integrated photoelasticity. in Photoelasticity of Glass 86–101 (Springer, 1993).

4.Gabor, D. A new microscopic principle. nature 161, 777–778 (1948).

5.Schnars, U., Falldorf, C., Watson, J. & Jüptner, W. Digital holography. in Digital Holography and Wavefront Sensing 39–68 (Springer, 2015).

6.Gorthi, S. S. & Rastogi, P. Fringe projection techniques: whither we are? Opt. Lasers Eng. 48, 133–140 (2010).

7.Pan, B., Qian, K., Xie, H. & Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review. Meas. Sci. Technol. 20, 062001 (2009).

8.Marr, D. & Poggio, T. A computational theory of human stereo vision. Proc. R. Soc. Lond. B Biol. Sci. 204, 301–328 (1979).

9.Pitas, I. Digital image processing algorithms and applications. (John Wiley & Sons, 2000).

10.Trusiak, M., Patorski, K. & Wielgus, M. Adaptive enhancement of optical fringe patterns by selective reconstruction using FABEMD algorithm and Hilbert spiral transform. Opt. Express 20, 23463–23479 (2012).

11.Awatsuji, Y. et al. Single-shot phase-shifting color digital holography. in LEOS 2007-IEEE Lasers and Electro-Optics Society Annual Meeting Conference Proceedings 84–85 (IEEE, 2007).

12.Fusiello, A., Trucco, E. & Verri, A. A compact algorithm for rectification of stereo pairs. Mach. Vis. Appl. 12, 16–22 (2000).

13.Zuo, C. et al. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Lasers Eng. 109, 23–59 (2018).

14.Zuo, C., Huang, L., Zhang, M., Chen, Q. & Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 85, 84–103 (2016).

15.Konolige, K. Small vision systems: Hardware and implementation. in Robotics research 203–212 (Springer, 1998).

16.Hong, C. K., Ryu, H. S. & Lim, H. C. Least-squares fitting of the phase map obtained in phase-shifting electronic speckle pattern interferometry. Opt. Lett. 20, 931–933 (1995).

17.Zuo, C., Chen, Q., Qu, W. & Asundi, A. Phase aberration compensation in digital holographic microscopy based on principal component analysis. Opt. Lett. 38, 1724–1726 (2013).

18.Langehanenberg, P., Kemper, B., Dirksen, D. & Von Bally, G. Autofocusing in digital holographic phase contrast microscopy on pure phase objects for live cell imaging. Appl. Opt. 47, D176–D182 (2008).

19.Wang, Y. & Zhang, S. Optimal fringe angle selection for digital fringe projection technique. Appl. Opt. 52, 7094–7098 (2013).

20.McCulloch, W. S. & Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5, 115–133 (1943).

21.Rosenblatt, F. The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386 (1958).

22.Rumelhart, D. E., Hinton, G. E. & Williams, R. J. Learning representations by back-propagating errors. nature 323, 533–536 (1986).

23.LeCun, Y. et al. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1, 541–551 (1989).

24.Hinton, G. E., Osindero, S. & Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 18, 1527–1554 (2006).

25.Krizhevsky, A., Sutskever, I. & Hinton, G. E. ImageNet classification with deep convolutional neural networks. Commun. ACM 60, 84–90 (2017).

26.Nair, V. & Hinton, G. E. Rectified linear units improve restricted boltzmann machines. in ICML (2010).

27.Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R. R. Improving neural networks by preventing co-adaptation of feature detectors. ArXiv Prepr. ArXiv12070580 (2012).

28.Chen, J. X. The evolution of computing: AlphaGo. Comput. Sci. Eng. 18, 4–7 (2016).

29.LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).

30.Ouyang, W. et al. DeepID-Net: Object detection with deformable part based convolutional neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 39, 1320–1334 (2016).

31.Doulamis, N. & Voulodimos, A. FAST-MDL: Fast Adaptive Supervised Training of multi-layered deep learning models for consistent object tracking and classification. in 2016 IEEE International Conference on Imaging Systems and Techniques (IST) 318–323 (IEEE, 2016).

32.Dong, C., Loy, C. C., He, K. & Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 38, 295–307 (2015).

33.Long, J., Shelhamer, E. & Darrell, T. Fully convolutional networks for semantic segmentation. in Proceedings of the IEEE conference on computer vision and pattern recognition 3431–3440 (2015).

34.Ronneberger, O., Fischer, P. & Brox, T. U-net: Convolutional networks for biomedical image segmentation. in International Conference on Medical image computing and computer-assisted intervention 234–241 (Springer, 2015).

35.Yan, K. et al. Fringe pattern denoising based on deep learning. Opt. Commun. 437, 148–152 (2019).

36.Shi, J., Zhu, X., Wang, H., Song, L. & Guo, Q. Label enhanced and patch based deep learning for phase retrieval from single frame fringe pattern in fringe projection 3D measurement. Opt. Express 27, 28929 (2019).

37.Kemao, Q. Windowed Fourier transform for fringe pattern analysis. Appl. Opt. 43, 2695–2702 (2004).

38.Takeda, M., Ina, H. & Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. JosA 72, 156–160 (1982).

39.Feng, S. et al. Fringe pattern analysis using deep learning. Adv. Photonics 1, 025001 (2019).

40.Feng, S., Zuo, C., Yin, W., Gu, G. & Chen, Q. Micro deep learning profilometry for high-speed 3D surface imaging. Opt. Lasers Eng. 121, 416–427 (2019).

41.Qian, J. et al. Deep-learning-enabled geometric constraints and phase unwrapping for single-shot absolute 3D shape measurement. APL Photonics 5, 046105 (2020).

42.Tao, T. et al. Real-time 3-D shape measurement with composite phase-shifting fringes and multi-view system. Opt. Express 24, 20253 (2016).

43.An, Y., Hyun, J.-S. & Zhang, S. Pixel-wise absolute phase unwrapping using geometric constraints of structured light system. Opt. Express 24, 18445–18459 (2016).

44.Tao, T. et al. High-speed real-time 3D shape measurement based on adaptive depth constraint. Opt. Express 26, 22440 (2018).

45.Zˇbontar, J. & LeCun, Y. Stereo matching by training a convolutional neural network to compare image patches. 32.

46.Mei, X. et al. On building an accurate stereo matching system on graphics hardware. in 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops) 467–474 (IEEE, 2011).

47.Pang, J., Sun, W., Ren, J. SJ., Yang, C. & Yan, Q. Cascade Residual Learning: A Two-Stage Convolutional Neural Network for Stereo Matching. in 2017 IEEE International Conference on Computer Vision Workshops (ICCVW) 878–886 (IEEE, 2017). doi:10.1109/ICCVW.2017.108.

48.Montresor, S., Tahon, M., Laurent, A. & Picart, P. Computational de-noising based on deep learning for phase data in digital holographic interferometry. APL Photonics 5, 030802 (2020).

49.Li, Z., Shi, Y., Wang, C., Qin, D. & Huang, K. Complex object 3D measurement based on phase-shifting and a neural network. Opt. Commun. 282, 2699–2706 (2009).

50.Li, Z., Shi, Y., Wang, C. & Wang, Y. Accurate calibration method for a structured light system. Opt. Eng. 47, 053604 (2008).

51.Feng, S., Zuo, C., Hu, Y., Li, Y. & Chen, Q. Deep-learning-based fringe-pattern analysis with uncertainty estimation. Optica 8, 1507–1510 (2021).

文章轉載/商務合作/課題組投稿，微信：447882024

帶您每天讀1篇文獻！加入>Light讀書會