2015年5月24日，演員袁立在新浪微博上如是說：“【X光線的由來】第一位諾貝爾物理學獎獲得者、德國科學家倫琴，當他發現射線后，并沒有以自己的名字去命名，而是根據《圣經》希伯來書第四章第十二節的內容，取希臘文‘基督’的第一個字母X為名，稱為X射線，或稱為X光，即基督耶穌之光。”

        純粹的假話非常容易被看穿，因此有經驗的謊言制造者往往會制造七分真三分假的假話。這種假話表面上非常合理可信，而這次這位明星似乎就因此而不幸中招了。

真實的χριστ??

        眾所周知，希臘在古典時代并不信仰基督教，而是信奉以宙斯為首的奧林匹斯諸神。希臘基督教化得到羅馬時代，受到東方影響。因此，雖然希臘是后來西方基督教文化的重要源頭，希臘語也為西方基督教很多概念提供了詞匯，如英語中的bible（圣經）、church（教堂）皆來自希臘語，但是希臘自己對宗教概念的表述也受到東方語言的影響。

        希臘語中把耶穌基督稱為Χριστ??，這個詞實際上是“受膏者”之義，是希臘人對希伯來語Mā??a?的翻譯，相當于耶穌的一個頭銜。故而說在希臘語中基督的第一個字母是Χ是正確的，只是這個X在使用拉丁字母的語言中，并不常用X來對，而往往采用Ch，因此拉丁語中耶穌基督是Christus，并不是Xristus，英語的Christ拼寫來自拉丁語，自然也是繼承了拉丁語的寫法。

        拉丁字母源自希臘字母，絕大多數拉丁字母都可以和希臘字母建立一一對應的關系。希臘的Α（alpha）Β（beta）Γ（gamma）Δ（delta）和拉丁字母ABCD的關系一目了然。但是為何Χ（chi）是個例外呢？

        拉丁字母來自伊特魯斯坎字母，后者脫胎于古希臘字母的西部變體，因此和后來通行的東部變體有一定差別。其中一項就是Χ在西部用來表示ks，而在東部用來表示kh。在羅馬人和希臘世界建立密切聯系后，用表示ks的X來代表希臘語字母Χ（chi）顯然并不合適，于是羅馬人就采用ch的拼寫予以對應。

        

        也因此，雖然拉丁字母X在采用拉丁字母表的語言中普遍讀ex，但是在X作為希臘字母出現的時候一般卻讀作chi。比較常見的一種Χριστ??的縮寫是把首兩字母疊加在一起寫為?，這種符號一般用在羅馬軍團的拉布蘭旗上，不過這個符號卻是按照希臘字母的讀法讀作Chi Rho的。隨著時代的演進，后來在英語中有進一步簡化Chi Rho，而用Xmas Xian代表Christmas Christian的，現在也有人把這種縮寫中的X按照一般的拉丁字母讀法來讀，只是這種讀法并不正式。

        

        因此，假如X光真的是來自希臘語“耶穌基督”的話，那么它的讀法大概更有可能按照希臘字母的習慣讀為Chi光，而不是現在的Ex光。        

未知的X

        事實上，X射線叫X射線，和耶穌基督的關系微乎其微。

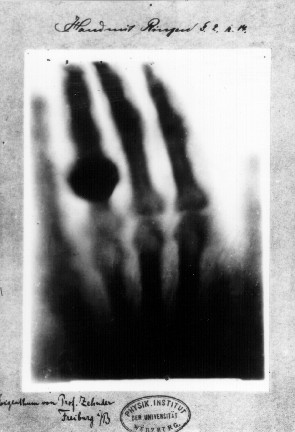
        德國物理學家倫琴于1895年發現了X射線。他是第一個系統研究X射線的人，也正是倫琴將這項劃時代的新發現命名為X射線的。而他用X表示這種新發現，則是因為X被普遍用來表示未知的事物。

        在X射線剛發現的時代，雖然倫琴觀察到了這些射線造成的影響，但是對于X射線究竟由什么構成則尚未弄明白。作為一個具有良好數學基礎的物理學家，引用數學中未知數X的概念用以表示這個新興事物也是很順理成章的。

        

        那么，為什么X會被用來表示未知數呢？這個相沿已久的傳統是怎么來的？

        現代數學上用X表示未知數的習慣可追溯到17世紀的歐洲。

        當時的歐洲用來表示未知數的符號極其混亂。一種常見的方法是用N表示未知數，而用Q表示未知數的平方，C表示未知數的立方。但是同時還存在很多其他的表示法，如用l表示未知數，而用q、c、qq、qc等表示未知數的更高次方。

        將x確立為表示未知數的標準形式的，是法國數學家笛卡爾。

        作為當年解析幾何界的大師，笛卡爾在《幾何學》（《La Géométrie》）這部作品中用a b c表示已知數，而用x y z表示未知數。至于笛卡爾為什么選擇了字母表中最后三個字母來代表未知數，他并沒有給出明確的解釋。而且他本人的用法也頗為搖擺不定——他曾經用過A、B、C表示未知數，甚至在1640年——《幾何學》發表三年后，笛卡爾寫給友人的一封書信當中，尚有1C-6N=40的算式，用現代寫法寫則為x3-6x=40。

        不過自此之后，用x表示未知數的方法漸漸流行起來，并最終成為數學界共同遵循的規范。        

未知數在中國

        現代中國使用全世界通用的數學符號，但在跟西方接觸之前，中國人是怎么來表示未知數的呢？

        學過方程的人都知道“一元一次方程”、“二元一次方程”、“一元二次方程”等術語。稍加推想就可知道其中的“元”即為現代數學中的未知數。不過，未知數為何要叫“元”呢？

        中國把未知數叫做“元”，實際上來自宋元時期的天元術。

        天元術在中國古代主要用以建立二次以上的高次方程。金代數學家李冶的《測圓海鏡》《益古演段》等書都大量使用天元術。而天元術的得名，正是因為天元術把未知數稱作“天元”。

        雖然比起現代代數，這種表示法多有不便，但是在當時已經是頗為了不起的成就。后來，在元朝的《四元玉鑒》中，朱世杰為了解多元高次方程，又引入了地元、人元、物元等另外三元。

        到了清朝，李善蘭和偉烈亞力翻譯了英國數學家德摩根的《代數學》，他們取材古代術語，創用了“多元一次方程”之類的術語。于是，“元”作為漢語中表示未知數的字的地位愈發鞏固，不過在列算式時，卻終究抵擋不住x的入侵了。