原創(chuàng) Tony Liu等 集智俱樂部 收錄于話題#因果科學(xué)19個

導(dǎo)語

在許多數(shù)據(jù)科學(xué)問題中，由觀測數(shù)據(jù)估計因果關(guān)系是一項(xiàng)極具挑戰(zhàn)但又十分必要的環(huán)節(jié)。最近一篇發(fā)表于 Nature Computational Science 的論文《用準(zhǔn)實(shí)驗(yàn)量化數(shù)據(jù)科學(xué)中的因果關(guān)系》回顧了計量經(jīng)濟(jì)學(xué)中常用的方法：基于觀察數(shù)據(jù)、利用數(shù)據(jù)的隨機(jī)波動——即借助準(zhǔn)實(shí)驗(yàn)判定因果關(guān)系的方法。同時，作者展示了如何將該方法與機(jī)器學(xué)習(xí)相結(jié)合，在典型的數(shù)據(jù)科學(xué)環(huán)境中回答因果問題。該文還強(qiáng)調(diào)了數(shù)據(jù)科學(xué)家如何能夠幫助推進(jìn)這些方法，從而對來自醫(yī)學(xué)、工業(yè)和社會中的高維數(shù)據(jù)進(jìn)行因果估計。

集智俱樂部聯(lián)合智源社區(qū)，組織，從基礎(chǔ)和實(shí)操角度出發(fā)，精讀兩本因果科學(xué)方向的入門教材。詳情見文末。

Tony Liu, Lyle Ungar & Konrad Kording | 作者

郭瑞東 | 譯者

趙雨亭、黃俊銘 | 審校

鄧一雪 | 編輯

論文題目：

Quantifying causality in data science with quasi-experiments

論文地址：

https://www.nature.com/articles/s43588-020-00005-8

目錄

1、準(zhǔn)實(shí)驗(yàn)方法判定因果的目標(biāo)

2、觀測研究中的混雜因子和碰撞因子

3、準(zhǔn)實(shí)驗(yàn)策略之工具變量估計

4、準(zhǔn)實(shí)驗(yàn)策略之?dāng)帱c(diǎn)回歸

5、準(zhǔn)實(shí)驗(yàn)策略之雙重差分

6、 準(zhǔn)實(shí)驗(yàn)的局限性

7、數(shù)據(jù)科學(xué)可以受益于準(zhǔn)實(shí)驗(yàn)，準(zhǔn)實(shí)驗(yàn)可以從機(jī)器學(xué)習(xí)中獲益

1. 準(zhǔn)實(shí)驗(yàn)方法判定因果的目標(biāo)

盡管大多數(shù)數(shù)據(jù)科學(xué)都集中于使用統(tǒng)計學(xué)和機(jī)器學(xué)習(xí)的工具來進(jìn)行預(yù)測[1]，并從數(shù)據(jù)中“提取洞見”，但許多問題根源都是因果關(guān)系，模型所做的預(yù)測和所獲得的洞見，被用來為決策提供信息。例如，數(shù)據(jù)科學(xué)家可以建立一個機(jī)器學(xué)習(xí)模型來預(yù)測哪些患者可能在30天內(nèi)再次入院，但利益相關(guān)者最終想知道可以采取哪些干預(yù)或政策，以便降低患者再次入院的風(fēng)險。數(shù)據(jù)科學(xué)家需要在他們的工具包中添加因果方法，以回答他們打算解決的許多問題中的因果問題。

由于相關(guān)性不足以構(gòu)成因果關(guān)系，因此將數(shù)據(jù)科學(xué)分析中，將常見的相關(guān)結(jié)果誤解為因果關(guān)系是危險的。任何典型的有監(jiān)督的機(jī)器學(xué)習(xí)方法（例如，基于一組特征的預(yù)測）都不足以推斷因果關(guān)系，因?yàn)橛糜陬A(yù)測的機(jī)器學(xué)習(xí)模型訓(xùn)練本質(zhì)上是一個相關(guān)性的任務(wù)：機(jī)器學(xué)習(xí)模型在做出預(yù)測時只是“觀察”數(shù)據(jù)中的特征和結(jié)果之間的關(guān)系，而非“改變”特征來確定它們對結(jié)果的影響[2, 3]。

一個例子：某個用來預(yù)測肺炎患者死亡率的模型得出了一個矛盾的結(jié)論，即哮喘降低了肺炎患者的死亡率[4]。這個模型沒有任何錯誤：在訓(xùn)練數(shù)據(jù)中，有哮喘的病人更有可能住進(jìn)醫(yī)院、接受更積極的治療，最終導(dǎo)致較低的死亡率。然而，從決策的角度來看，該模型可能有害，因?yàn)樵谶@種預(yù)測下，可能會使哮喘病人得不到他們實(shí)際需要的額外護(hù)理。傳統(tǒng)的機(jī)器學(xué)習(xí)總是存在一種風(fēng)險：那就是未觀察到的特征可能正是決定性因素。

已有很多方法，以更適當(dāng)?shù)貜挠^測數(shù)據(jù)（沒有隨機(jī)對照實(shí)驗(yàn)的情況下）來估計因果關(guān)系。該文回顧了標(biāo)準(zhǔn)的準(zhǔn)實(shí)驗(yàn)方法，這些方法已經(jīng)在經(jīng)濟(jì)學(xué)中得到了廣泛的應(yīng)用；但并未在經(jīng)濟(jì)學(xué)以外廣為人知。該文討論了它們的假設(shè)，為什么這些方法應(yīng)該被更廣泛地采用，并用現(xiàn)實(shí)世界的例子以及公共數(shù)據(jù)科學(xué)領(lǐng)域的潛在應(yīng)用來說明作者的觀點(diǎn)。最后，該文提倡準(zhǔn)實(shí)驗(yàn)方法和數(shù)據(jù)科學(xué)的交叉結(jié)合：準(zhǔn)實(shí)驗(yàn)可以在典型的數(shù)據(jù)科學(xué)環(huán)境中進(jìn)行因果推斷，而機(jī)器學(xué)習(xí)的創(chuàng)新反過來可以改進(jìn)這些方法，以便在復(fù)雜的數(shù)據(jù)領(lǐng)域中得到更廣泛的應(yīng)用。

2. 觀測研究中的混雜因子和碰撞因子

觀測數(shù)據(jù)對因果推斷來說的核心問題存在不被觀測到的混淆因素。人們希望確定治療 x（住院）對結(jié)果 y （肺炎風(fēng)險）的影響，但是有一個隱藏的混淆因子 z（哮喘）同時影響 x 和 y。如果研究人員可以進(jìn)行一個實(shí)驗(yàn)：自行確定X的取值（即令X為自由變量），然后借此消除混淆因素、從而識別 x 對 y 的因果效應(yīng)（圖1a）。實(shí)驗(yàn)應(yīng)用于醫(yī)學(xué)（臨床試驗(yàn)）、公共衛(wèi)生（俄勒岡州醫(yī)療補(bǔ)助彩票試驗(yàn)[5]）、軟件開發(fā)和廣告（a/b 測試）、以及 ML（強(qiáng)化學(xué)習(xí)[6, 7, 8]）。然而，實(shí)驗(yàn)可能代價高昂、違反道德或者不切實(shí)際。此外，大多數(shù)數(shù)據(jù)是基于數(shù)據(jù)科學(xué)觀察得出的，但科研人員仍然想要估計因果效應(yīng)。要從觀測數(shù)據(jù)中推斷因果關(guān)系，通常需要對數(shù)據(jù)生成過程做不可檢驗(yàn)的假設(shè)。

圖1. 估計實(shí)驗(yàn)和觀測數(shù)據(jù)中因果關(guān)系的圖示法。圖A，一個實(shí)驗(yàn)研究的圖形表示，因?yàn)?x 是隨機(jī)的，導(dǎo)致治療 x 和混淆因子z 無關(guān)。圖B，觀察性研究的圖形表示，在這里碰撞因子 c 和混雜因子 z 都可以導(dǎo)致對因果效應(yīng)的估計出現(xiàn)偏差。

許多從觀察數(shù)據(jù)中估計因果關(guān)系的技術(shù)都依賴于假設(shè)所有的混雜因素（影響治療 x 和結(jié)果 y 的變量）都在數(shù)據(jù)中得到觀察與解釋[9]。在這種情況下，可以控制混雜因素以獲得有效的因果估計——例如，通過將它們加入回歸。然而，研究人員通常不能知道自己是否記錄了所有的混雜因素[10]，因此需要對這個假設(shè)放置在重要權(quán)重上（圖1b）。從業(yè)者必須解釋，他們的數(shù)據(jù)實(shí)際上包含所有相關(guān)的混雜因素（而且沒有一個碰撞因子），對依賴于混雜因素的分析的批評往往集中在分析中包含缺失變量上。因?yàn)闆]有辦法檢驗(yàn)缺失變量是否是混雜因素，因果估計的信念取決于混雜因素假設(shè)是否可信。

例如，假設(shè)在本次肺炎風(fēng)險問題中，研究人員分析衡量病人的哮喘并控制病情。這項(xiàng)研究可能會被挑刺：還有許多其他潛在的混雜因素沒有被考慮在內(nèi)，比如種族、社會經(jīng)濟(jì)地位、吸煙狀況、其他病史等等。即使更多的這些潛在的混淆因素被作為研究的一部分進(jìn)行測量并加以控制，依然可能有別的因素沒有考慮到，這可能會威脅到結(jié)果的有效性。任何使用觀測數(shù)據(jù)做因果主張的研究，要么使用不依賴于混雜因子的方法，要么需要提供一個令人信服的論據(jù)，證明混雜性至少是近似正確的。

除了混雜因子，數(shù)據(jù)科學(xué)家還必須能夠識別那些不應(yīng)該被控制的變量，即所謂的碰撞因子。與同時影響 x 和 y 的混雜因素不同，碰撞因子是受 x 和 y 影響的變量（圖1b）。對碰撞因子的控制使研究人員的因果估計出錯[11, 12]。例如，他們可以想象在肺炎問題中的一種可能性，即哮喘本身是住院（x）和肺炎（y）的對撞因子：肺炎可能使住院病人更有可能出現(xiàn)哮喘癥狀，也可能是由于住院期間遭遇過敏。除了測量相關(guān)變量以控制混雜，尋求因果估計的數(shù)據(jù)科學(xué)家需要確保被控制的變量不是碰撞因子。

Judea Pearl 推廣的結(jié)構(gòu)因果模型（SCM）是計算機(jī)科學(xué)中一個常用的因果推斷框架[11]。SCM 將有向無環(huán)圖（DAGs）結(jié)合起來，用一個數(shù)學(xué)框架來表達(dá)因果關(guān)系，該數(shù)學(xué)框架用于計算來自 DAG 的因果量，稱為 do-calculus。結(jié)構(gòu)因果模型的美妙之處在于，一個問題的因果結(jié)構(gòu)可以用圖形表示，從而使因果效應(yīng)的假設(shè)和可識別性能更容易理解[13]。

需要有領(lǐng)域知識才能構(gòu)建結(jié)構(gòu)因果模型中的DAG，并證明在假設(shè)的圖表中沒有缺少混雜因素[3]。雖然研究人員可以通過檢查數(shù)據(jù)中是否反映了變量之間的隱含條件獨(dú)立性[2]，來在一定程度上檢驗(yàn)圖中變量之間的聯(lián)系的正確性，但是不包含混淆因素通常是不可檢驗(yàn)的[14]。除非人們對假設(shè)的DAG 的準(zhǔn)確性有強(qiáng)烈的堅(jiān)持，否則總會存在未被觀察到的混雜因素導(dǎo)致可能的因果估計偏差。

還有許多其他技術(shù)旨在從觀測數(shù)據(jù)中估計因果效應(yīng)，盡管它們常常依賴于非混淆假設(shè)及其變體。匹配和逆概率加權(quán)是社會科學(xué)中常用的兩種方法，可以用來控制因果估計中的混雜偏差[12, 15]。機(jī)器學(xué)習(xí)方法將處理效果treatment effect估計轉(zhuǎn)換為兩個預(yù)測任務(wù)，允許在高維數(shù)據(jù)中進(jìn)行因果推斷[16]。

在最近的機(jī)器學(xué)習(xí)領(lǐng)域[18, 19, 20]的活躍研究中，還有一個關(guān)于因果發(fā)現(xiàn)[17]的熱點(diǎn)領(lǐng)域，目標(biāo)是從數(shù)據(jù)本身推斷出因果關(guān)系圖：研究人員通常使用無混淆因子作為一種假設(shè)。潛變量模型也被應(yīng)用于觀察性因果推斷，它不要求不包含混淆因子，但確實(shí)需要對影響結(jié)果的原因的獨(dú)立性和數(shù)量作出具體的假設(shè)[21]。因?yàn)樵诂F(xiàn)實(shí)世界的問題中，無混雜因子通常很難被證明是正確的，所以科學(xué)家們選擇在這里強(qiáng)調(diào)準(zhǔn)實(shí)驗(yàn)策略。

3. 準(zhǔn)實(shí)驗(yàn)策略之工具變量估計

準(zhǔn)實(shí)驗(yàn)是經(jīng)濟(jì)學(xué)領(lǐng)域的已經(jīng)成熟的觀測因果關(guān)系的框架，利用觀測數(shù)據(jù)中自然存在的隨機(jī)性來估計因果效應(yīng)。過去幾十年間[22, 23]，經(jīng)濟(jì)學(xué)家越來越多地使用準(zhǔn)實(shí)驗(yàn)技術(shù)來估計現(xiàn)實(shí)世界的因果效應(yīng)。這些方法也依賴于對數(shù)據(jù)因果結(jié)構(gòu)的假設(shè)，但是這些假設(shè)可能比不包含混亂因子更合理。下面，本文回顧利用自然發(fā)生的隨機(jī)性來估計因果效應(yīng)。

第一個方法稱為工具變量估計[24]，旨在尋找工具變量，它產(chǎn)生的影響必須通過我們關(guān)心的 X 來實(shí)現(xiàn)（圖2a）。換句話說，研究人員不是要求系統(tǒng)不包括混淆因子，而是要求其某個組成部分不包含混淆因子，然后用它來估計因果關(guān)系。

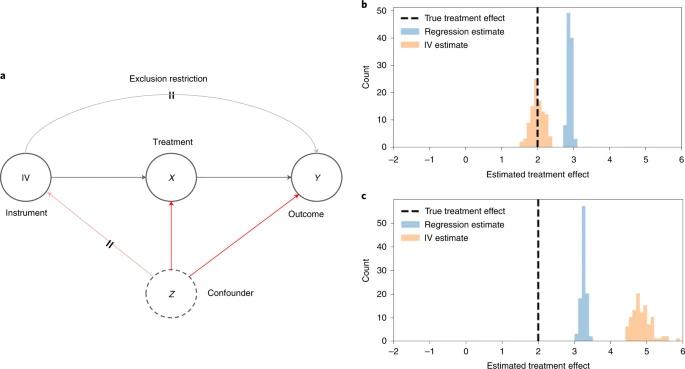
圖2. 在有向無環(huán)圖中的表示工具變量IV 如何影響x 對 y 的因果影響

圖A：交叉邊描述了有效的工具變量推斷所需的假設(shè): 無關(guān)假設(shè)（交叉灰邊）以及工具變量和 y 之間沒有未測量的混雜（交叉紅邊）。當(dāng) x 對 y 的真實(shí)處理效果（虛線）混淆時。圖B：用100個模擬數(shù)據(jù)集對工具變量（橙色）和典型回歸（藍(lán)色）的因果效果直方圖進(jìn)行估計。圖C：當(dāng) x 對 y 的真實(shí)處理效果（虛線）存在混淆因子并違反無關(guān)假設(shè)時，用100個模擬數(shù)據(jù)集對 IV （橙色）和典型回歸（藍(lán)色）的因果效果直方圖進(jìn)行估計。

經(jīng)濟(jì)學(xué)中工具變量分析（IV analysis）的一個著名例子考慮了以出生季節(jié)（z）為工具變量的必修課程（x）對個人未來工資（y）的影響[25]。在美國的許多州，兒童被要求在他們六歲的時候進(jìn)入學(xué)校，所以在這一年晚些時候出生的人在他們的學(xué)校該年級中，相對年輕。由于州法律要求學(xué)生在某一特定年齡之前都要上學(xué)（例如16歲），因?yàn)槌錾竟?jié)的不同，個人被要求上學(xué)的時間也不同。只要研究人員能夠假設(shè)出生季節(jié)實(shí)際上是隨機(jī)的，并且其對未來工資的影響必須通過教育水平來實(shí)現(xiàn)，那么出生季節(jié)就可以作為一種估計因果影響的工具。

為了使用工具變量分析因果關(guān)系，必須確定干預(yù)（要求的學(xué)校教育）、結(jié)果（未來工資）和工具變量（出生季節(jié)），并假定工具變量只通過對干預(yù)的影響來影響結(jié)果。然后，研究人員通常執(zhí)行所謂的兩階段最小二乘法[26]，也已經(jīng)提出了替代工具變量分析框架[27]：在第一階段（

，其中 α 是擬合系數(shù)）對工具變量的處理進(jìn)行回歸，然后根據(jù)第一階段（

，其中 β 是擬合系數(shù)）的處理估計結(jié)果進(jìn)行回歸。第一階段由于工具變量的影響，提取了干預(yù)中‘不包括混淆因子的部分’，并在研究人員的第二階段回歸中使用這個成分來估計對結(jié)果的因果影響，從而控制了過程中的混淆因子：圖2b 描述了混淆 x 對 y 的真正治療效果的模擬數(shù)據(jù)，可以看到在即使存在混淆因子的因果圖中，工具變量分析也給出了不偏不倚的因果估計。另一個令人鼓舞的例子，研究人員可以把前文提到的肺炎患者住院場所與家庭之間距離作為工具變量[28]（因?yàn)榫嚯x醫(yī)院多遠(yuǎn)似乎是隨機(jī)的）。

在進(jìn)行工具變量分析時，需要作出一些假設(shè)，以確保有效的估計。研究人員需要假設(shè)沒有混淆變量同時影響工具變量本身和結(jié)果 y（圖2a），這類似于不存在混淆因子的假設(shè)，但往往更有道理，因?yàn)楣ぞ叩倪x擇是隨機(jī)的：論證出生季節(jié)與未來的工資是無關(guān)的結(jié)論，比論證政府干預(yù) x ，即學(xué)校教育與未來的工資是無關(guān)的更合理。研究人員還需要確保工具變量只通過其對干預(yù)的影響影響系統(tǒng)，即所謂的無關(guān)假設(shè)（圖2a）：圖2c 描述了模擬數(shù)據(jù)，其中 x 對 y 的真實(shí)干預(yù)效果是包含混淆因子的，并且無關(guān)假設(shè)也不符合的。研究人員發(fā)現(xiàn)，無論是工具變量分析 還是回歸分析，都沒有給出正確的因果估計。

工具變量分析要求的另一個關(guān)鍵假設(shè)是單調(diào)性或無關(guān)假設(shè)：當(dāng)受到工具變量的影響時，研究人員的數(shù)據(jù)樣本中沒有患者接受了反向治療[29]。在上面的例子中，如果一些州違背了國家的政策，阻止年齡較晚的個人進(jìn)入學(xué)校，這將產(chǎn)生與其他州相反的效果。此外，成功的工具變量必須與干預(yù)密切相關(guān)，因?yàn)槿跸嚓P(guān)的工具變量缺乏精確度，無法產(chǎn)生實(shí)際上有用的估計。必須確保這些假設(shè)得到滿足，違反任何這些假設(shè)都可能威脅到結(jié)論的可信度。

例如，雖然天氣是工具變量分析中常用的工具變量[29, 30]——因?yàn)樘鞖獾淖兓坪跏请S機(jī)的——但它可能并不總是合適，這取決于具體的因果問題。對一位行為科學(xué)家而言，他希望研究鍛煉對心理健康的影響，并計劃利用氣溫作為衡量個人鍛煉量的工具變量。雖然這很直觀（溫度使得個人鍛煉的數(shù)量可以隨機(jī)出現(xiàn)），但實(shí)際上溫度可能與鍛煉只有微弱的相關(guān)性（例如，人們傾向于在室內(nèi)鍛煉，所以室外溫度不是很重要）；或者更令人擔(dān)憂的是，這可能違反了無關(guān)假設(shè)（溫度也可能經(jīng)由鍛煉之外影響心理健康，例如通過季節(jié)性情緒失調(diào)）。在這種情況下，雖然天氣似乎是一個很好的工具變量，仔細(xì)考慮便會發(fā)現(xiàn)該設(shè)計是有缺陷的。

只要我們找到一個合適的工具，使這些假設(shè)看似合理，工具變量分析可以廣泛用于許多學(xué)科，以利用可觀測的隨機(jī)性來源估計非實(shí)驗(yàn)數(shù)據(jù)的因果效應(yīng)（表1）。

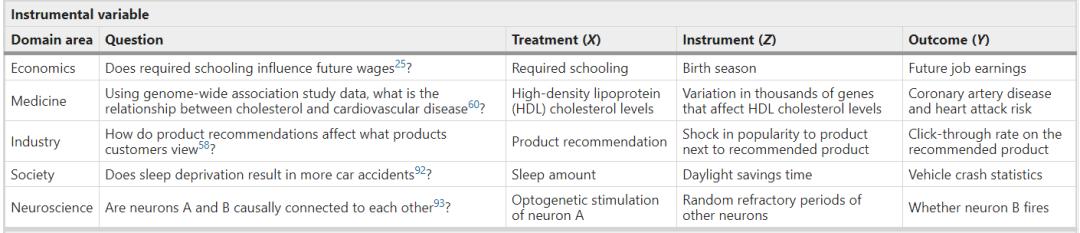
表1. 準(zhǔn)實(shí)驗(yàn)的現(xiàn)有研究和機(jī)會

4. 準(zhǔn)實(shí)驗(yàn)策略之?dāng)帱c(diǎn)回歸

利用自然發(fā)生的隨機(jī)性來估計因果關(guān)系的另一種方法是斷點(diǎn)回歸（Regression discontinuity designs）[32]。在斷點(diǎn)回歸中，干預(yù)變量X是某一連續(xù)變量R的跳躍點(diǎn)，其中R可能是年齡、考試或血壓讀數(shù)。因?yàn)樘S點(diǎn)并非漸變（例如，如果年齡在50歲或以上，患者得到癌癥篩查，抑或是沒有得到），x 值是準(zhǔn)隨機(jī)的，可允許對干預(yù) x 對結(jié)果 y 的因果影響進(jìn)行估計（圖3a）。

圖3. 斷點(diǎn)分析示意圖（Regression discontinuity designs）

上圖A：描述斷點(diǎn)分析如何使用連續(xù)變量 R 中的閾值 t 有效地隨機(jī)化處理 x （交叉紅線）來估計其對Y的因果效應(yīng)。圖B：結(jié)果Y對連續(xù)變量R的散點(diǎn)（藍(lán)點(diǎn)）和局部回歸擬合（紅線）。擬合分別使用斷點(diǎn)（虛線）左右兩側(cè)的線性模擬數(shù)據(jù)。圖C：結(jié)果Y對連續(xù)變量R的散點(diǎn)（藍(lán)點(diǎn)）和局部回歸擬合（紅線）。擬合分別使用斷點(diǎn)（虛線）左右兩側(cè)的非線性模擬數(shù)據(jù)。

斷點(diǎn)分析的典型例子是關(guān)于高中的學(xué)術(shù)證書（x）及其對后來的學(xué)術(shù)成就的影響——如是否獲得獎學(xué)金（y）。美國高中生參加一個標(biāo)準(zhǔn)化考試，即國家優(yōu)秀獎學(xué)金資格考試(NMSQT) ，滿足最低分?jǐn)?shù)線的學(xué)生將獲得全國認(rèn)可的優(yōu)秀證書。這里的連續(xù)變量是 NMSQT 測試分?jǐn)?shù)（r）。剛剛達(dá)到截止分?jǐn)?shù)的學(xué)生與剛剛錯過截止分?jǐn)?shù)的學(xué)生沒有實(shí)質(zhì)上的區(qū)別，本質(zhì)上是隨機(jī)分配接近截止分?jǐn)?shù)的優(yōu)異證書。這種半隨機(jī)化的設(shè)計可以估計優(yōu)異證書與接受閾值附近的學(xué)生獎學(xué)金之間的因果關(guān)系。在前文提到的醫(yī)療場景下，使用肺炎風(fēng)險評分，與閾值判定是否住院的數(shù)據(jù)，通過斷點(diǎn)分析，也可用于進(jìn)行因果估計。

使用斷點(diǎn)分析獲得因果估計的一個常用方法是在閾值的左右兩側(cè)擬合運(yùn)行變量 r （測試分?jǐn)?shù)）的結(jié)果 y （獎學(xué)金數(shù)額）的兩個模型，稱為線性情況下的局部線性回歸（圖3b 描述模擬數(shù)據(jù)的局部線性回歸）[34, 35]。閾值 x （優(yōu)異證書）的因果效應(yīng)大小等于兩個擬合回歸方程在閾值左右的預(yù)測值的差異。實(shí)現(xiàn)斷點(diǎn)分析的一個實(shí)際考慮考慮帶寬規(guī)模：一個人距離能夠并且仍然能夠有效地進(jìn)行隨機(jī)處理的臨界值有多遠(yuǎn)？較小的帶寬使準(zhǔn)隨機(jī)處理更為可信，但也減少了擬合回歸的樣本容量。然而，更大的帶寬可能會在我們的估計中引入偏差，特別是如果斷點(diǎn)變量 r 和結(jié)果 y 之間的關(guān)系是非線性的，如圖3C 中的模擬數(shù)據(jù)所示：注意在閾值左右局部回歸之間的差異與結(jié)果 y 中的實(shí)際不連續(xù)變化不匹配。幸運(yùn)的是，計量經(jīng)濟(jì)學(xué)一直在探索最佳且由數(shù)據(jù)驅(qū)動的帶寬選擇方法bandwidth selection methods[36, 37]。在閾值兩側(cè)擬合局部模型利用了閾值處理的準(zhǔn)隨機(jī)性，使研究人員能夠量化因果效應(yīng)。

與工具變量分析類似，在執(zhí)行斷點(diǎn)分析時需要一些假設(shè)，以確保有效的估計。研究人員假設(shè)只有斷點(diǎn)變量 r 有一個不連續(xù)的跳躍，驅(qū)動干預(yù)和結(jié)果之間的因果關(guān)系（圖3a）。這個假設(shè)可以通過驗(yàn)證其他測量的協(xié)變量在 r 的截止值上的連續(xù)性而在實(shí)踐中被證偽。另一個關(guān)鍵的假設(shè)要求個體不能完全操縱斷點(diǎn)變量，因?yàn)檫@可能使閾值上下的群體無法比較。在研究人員上面的例子中，如果一些學(xué)生能夠精確地控制他們的考試成績，以至于他們僅僅通過足夠的學(xué)習(xí)就達(dá)到了優(yōu)秀證書的閾值，這將違反處理的準(zhǔn)隨機(jī)化。經(jīng)濟(jì)學(xué)家已經(jīng)為這種操縱變量的運(yùn)行是否存在開發(fā)了檢驗(yàn)方法，從而為驗(yàn)證該假設(shè)提供了可能[38]。值得注意的是，斷點(diǎn)回歸分析并不需要不包含混淆因素，才能做出有效的因果估計。由于其相對薄弱和經(jīng)常可證偽的假設(shè)，斷點(diǎn)分析被稱為最可靠的基于觀測數(shù)據(jù)估計因果關(guān)系的準(zhǔn)實(shí)驗(yàn)方法之一[39]。

然而，盡管每當(dāng)有一個確定干預(yù)與否的閾值時，嘗試和應(yīng)用斷點(diǎn)回歸分析是非常誘人，但是在一些似是而非的情況下，這些假設(shè)并不成立。在實(shí)踐中需要仔細(xì)考慮剛好高于或低于閾值的單位是否具有可比性這一假設(shè)，因?yàn)楫?dāng)研究中的個體知道閾值和分?jǐn)?shù)時，違規(guī)行為經(jīng)常出現(xiàn)。例如，一個人可以研究補(bǔ)助金對年輕科學(xué)家未來學(xué)術(shù)成就的影響，利用國立衛(wèi)生研究院的薪水線作為閾值研究補(bǔ)助金對學(xué)術(shù)成就的因果關(guān)系，進(jìn)行斷點(diǎn)回歸分析[40, 41]。然而，隨著薪水閾值的公布，很可能那些知道自己剛剛錯過閾值的科學(xué)家們比那些剛剛到達(dá)閾值的科學(xué)家們更有動力去努力工作，這可能會造成對未來成功的估計的偏差，因?yàn)閯倓偟竭_(dá)閾值上下的科學(xué)家們在動機(jī)上存在差異。

只要這些假設(shè)是合理的，斷點(diǎn)回歸分析就有可能廣泛地適用于因果效應(yīng)估計，因?yàn)樵谠S多現(xiàn)實(shí)數(shù)據(jù)設(shè)置中都存在閾值（表1），即使是在地理界限等非常規(guī)設(shè)置中也是如此[42]。

5. 準(zhǔn)實(shí)驗(yàn)策略之雙重差分

第三種標(biāo)準(zhǔn)的計量經(jīng)濟(jì)學(xué)方法稱為雙重差分（Difference-in-differences），通過觀察治療組和對照組，并比較他們隨著時間推移的結(jié)果趨勢，來解決觀察數(shù)據(jù)中的混雜因子。研究人員對接受干預(yù)的治療組和不接受治療的對照組在治療前（Y1）和治療后（Y2） x 的時間段內(nèi)的結(jié)果，對 y 進(jìn)行了測量。治療組的單純差異 Y2，治療 -Y1，治療可作為 x 的因果效應(yīng)的估計，但它可能被未觀察因素或時間效應(yīng)所混淆。雙重差分的思想是使用差異 Y2，控制 -Y1，控制組作為混雜影響治療組的估計，通過減去這第二個差異來校正這個影響（圖4a）。

圖4. 雙重差分法示意圖

圖A：雙重差分的圖形表示，其中控制組和治療組都受到混淆因子的 Z1 的影響，但他們在治療前和治療后的差異，可以對得到對結(jié)果 y 的無偏估計。研究人員必須選擇一個適當(dāng)?shù)目刂平M，使任何混雜因素都同時影響這兩組（圖A中只影響治療組的 Z2的虛線的存在將違反這一規(guī)定）。圖B：在模擬數(shù)據(jù)中，隨著時間的推移，治療組（橙色）和對照組（藍(lán)色）的結(jié)果 y 的散點(diǎn)圖（平行趨勢保持），干預(yù) x 被應(yīng)用于治療組（虛線）。圖C：在違反平行趨勢假設(shè)的模擬數(shù)據(jù)中，治療組（橙色）和對照組（藍(lán)色）隨時間的結(jié)果 y 散點(diǎn)圖。

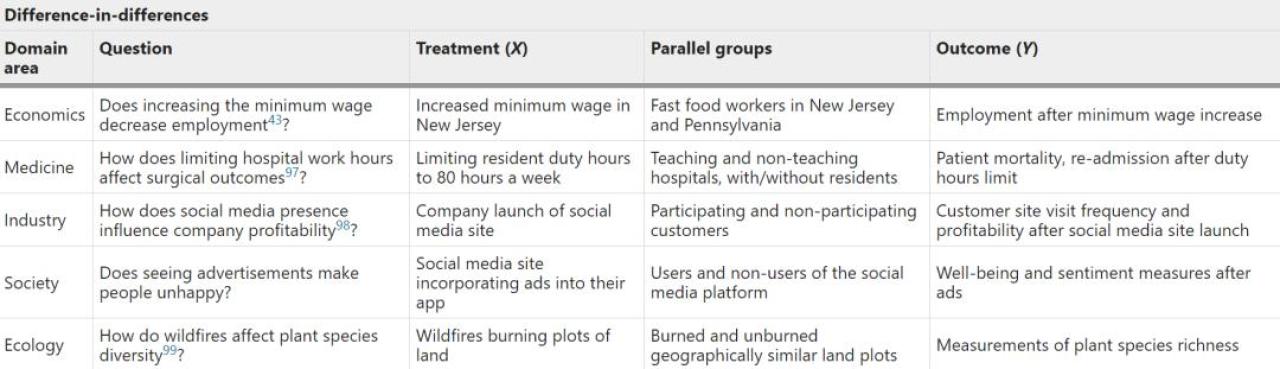
經(jīng)濟(jì)學(xué)中，使用雙重差分的經(jīng)典例子是關(guān)于提高最低工資（x）對就業(yè)（y）的影響[9, 43]。新澤西州在1992年提高了最低工資標(biāo)準(zhǔn)，而與之接壤的賓夕法尼亞州卻沒有。這項(xiàng)研究比較了政策改變前后，兩個州的快餐店就業(yè)人數(shù)。如果只考慮新澤西州，就業(yè)率的變化可能會受到其它因素的影響，比如全國性衰退。然而，通過減去在賓夕法尼亞州觀察到的就業(yè)差異，作者可以控制潛在的混雜因素。

為了進(jìn)行雙重差分分析，研究人員使用縱向數(shù)據(jù)來估計對照組和治療組的 Y1和 Y2（例如，最低工資前后的增長）。估計值可以是在前后時間段內(nèi)計算的單一期望值，或者，如果從業(yè)者希望包括多個時間點(diǎn)和對其他協(xié)變量的控制，可以使用時間序列回歸進(jìn)行估計[44, 45]。然后研究人員得到治療組和對照組之間結(jié)果值的估計差異。

，通過減去同樣影響對照組和治療組的混雜因素，得出干預(yù) x 對結(jié)果 y 的影響的有效估計：圖4B 直觀地描述了這一點(diǎn)，治療組和對照組的預(yù)處理趨勢線是平行的。研究人員在這里注意到，雙重差分是一種特殊的回歸方法，用以從時間序列中估計因果關(guān)系。雙重差分可用于非參數(shù)和非線性設(shè)定[46, 47, 48]。和雙重差分相關(guān)，綜合控制法（synthetic control）是經(jīng)濟(jì)學(xué)中發(fā)展起來的另一種從時間序列數(shù)據(jù)中估計因果效應(yīng)的方法[41]。

像其他的準(zhǔn)實(shí)驗(yàn)方法一樣，雙重差分需要滿足假設(shè)，來確保有效的因果估計。最重要的假設(shè)是平行趨勢的存在：研究人員要求被實(shí)驗(yàn)組和對照組不會隨著時間的推移受到混雜因素的不同影響。在上述最低工資的例子中，如果賓夕法尼亞州的勞動力市場與新澤西州的勞動力市場對持續(xù)衰退的反應(yīng)不同，那么這個平行的趨勢假設(shè)就會被打破。如果縱向數(shù)據(jù)包含多個時間點(diǎn)，平行趨勢假設(shè)可以通過在干預(yù) x 發(fā)生前檢查兩組的結(jié)果 y 是否存在差異來證偽，圖4C 直觀地描述了這一過程。

研究需要的另一個假設(shè)是不存在溢出效應(yīng)，即干預(yù)本身導(dǎo)致控制和受治療群體的組成不會發(fā)生變化[49]。如果新澤西州新的最低工資標(biāo)準(zhǔn)導(dǎo)致不同的人重新進(jìn)入就業(yè)市場，或者賓夕法尼亞州的人搬到新澤西州，這就違反了上述規(guī)定。另一個雙重差分假設(shè)被違反的例子是這項(xiàng)研究：該研究中，研究人員考察了美國向各國提供的糧食援助對隨后發(fā)生的國內(nèi)沖突的影響——美國小麥生產(chǎn)的隨機(jī)變化影響了向各國提供的援助數(shù)量[50]。問題在于，小麥生產(chǎn)與沖突之間的聯(lián)系隨著時間的推移而在“受到干預(yù)”和“不受干預(yù)”國家之間發(fā)生變化，這違反了平行趨勢的假設(shè)，并表明糧食援助對沖突的影響可能是由虛假的相關(guān)關(guān)系驅(qū)動的[51]。為了使雙重差分法有效，我們需要證據(jù)來支持平行趨勢假設(shè)，及不存在溢出效應(yīng)。

然而，雙重差分的透明性和靈活性使其成為一種有吸引力的因果推斷技術(shù)，前提是進(jìn)行了適當(dāng)?shù)目刂疲⑶译p重差分發(fā)的假設(shè)是合理的。由于許多數(shù)據(jù)科學(xué)問題涉及到時間序列，該方法有可能被廣泛用于從觀測數(shù)據(jù)中獲得因果估計。

6. 準(zhǔn)實(shí)驗(yàn)的局限性

使用準(zhǔn)實(shí)驗(yàn)技術(shù)所作的因果估計的概括性有其局限性。研究人員回顧的所有方法都是對特定人群的因果效應(yīng)進(jìn)行估計。個人自愿評估估計受工具變量的影響的個人的因果效應(yīng)[52]。斷點(diǎn)回歸 估計了個人在閾值時的因果效應(yīng)[53]。在更強(qiáng)有力的假設(shè)下，從閾值以外推斷因果效應(yīng)是可行的[54]。雙重差分法對選定的治療組的因果效應(yīng)進(jìn)行了估計。然而，研究人員注意到，對可泛化性的關(guān)注甚至延伸到了隨機(jī)化實(shí)驗(yàn)，即參與者的人口統(tǒng)計學(xué)可以將因果發(fā)現(xiàn)限制在一個特定的人群中[55]。當(dāng)應(yīng)用準(zhǔn)實(shí)驗(yàn)方法時，就像所有的因果分析一樣，研究人員必須留意這些估計對哪些人群是有效的。

一個實(shí)際的考慮是，準(zhǔn)實(shí)驗(yàn)需要一個特定的數(shù)據(jù)生成過程或觀察到應(yīng)用的特定類型的變量，例如與干預(yù)密切相關(guān)的工具變量、斷點(diǎn)回歸中閾值的存在與否；或是否存在一個適當(dāng)?shù)目刂平M隨著時間的推移，可與治療組進(jìn)行比較。因此，使用準(zhǔn)實(shí)驗(yàn)方法估計因果效應(yīng)取決于數(shù)據(jù)是否符合這些框架，因?yàn)槿藗兺ǔ２荒軐F(xiàn)有數(shù)據(jù)改造成這些方法中的一種：“實(shí)驗(yàn)設(shè)計勝過分析”[56]。

此外，在沒有適當(dāng)考慮技術(shù)的基礎(chǔ)假設(shè)的情況下，尋找適合這些設(shè)計的數(shù)據(jù)存在一些風(fēng)險，如果不滿足這些假設(shè)，分析可能會失效。正如上一節(jié)所討論的那樣，如果仔細(xì)考慮假設(shè)，從表面上看，似乎適合應(yīng)用這些方法的數(shù)據(jù)也可能不會奏效。

7. 數(shù)據(jù)科學(xué)可以受益于準(zhǔn)實(shí)驗(yàn)，

準(zhǔn)實(shí)驗(yàn)可以從機(jī)器學(xué)習(xí)中獲益

準(zhǔn)實(shí)驗(yàn)應(yīng)該更廣泛地應(yīng)用于數(shù)據(jù)科學(xué) ，因?yàn)樗鼈兪窃谠S多情況下有意義地估計因果關(guān)系的唯一方式。例如，工具變量分析被用來評估推薦系統(tǒng)的因果效應(yīng)[57]，即利用產(chǎn)品受歡迎程度中的隨機(jī)沖擊作為工具變量[58]。在流行病學(xué)中，一種流行的技術(shù)叫做孟德爾隨機(jī)化，它使用遺傳變異作為工具變量[59, 60]。斷點(diǎn)分析在醫(yī)療實(shí)踐中比比皆是，同時也應(yīng)該擴(kuò)展至更多應(yīng)用[61]。雙重差分法可以用來評估政策和執(zhí)行在諸如廣告[62]和公共健康[63]等各個領(lǐng)域的長期效果。準(zhǔn)實(shí)驗(yàn)策略可以估計在這些情況下的因果效應(yīng)，為決策提供有用的反饋。

此外，研究人員可以將這些準(zhǔn)實(shí)驗(yàn)中的因果估計與其他數(shù)據(jù)結(jié)合起來，以提高機(jī)器學(xué)習(xí)的性能。例如，在基于觀察研究中，已經(jīng)有使用重疊實(shí)驗(yàn)數(shù)據(jù)來控制混雜因子的工作，這可以擴(kuò)展到利用準(zhǔn)實(shí)驗(yàn)數(shù)據(jù)[64]。在與環(huán)境互動的過程中，強(qiáng)化學(xué)習(xí)執(zhí)行干預(yù)、做出決策和形成政策，這些都是固有的因果任務(wù)[11, 65]。

然而，現(xiàn)代的強(qiáng)化學(xué)習(xí)往往需要很昂貴的訓(xùn)練成本，因此納入準(zhǔn)實(shí)驗(yàn)的因果效應(yīng)估計可能是一個有希望的提高效率的方式[66]。特別是，為了優(yōu)化策略，已將斷點(diǎn)分析應(yīng)用于多臂老虎機(jī)問題[67]。隨著對因果關(guān)系的重新關(guān)注[69, 70]，人們對可解釋的人工智能[68]產(chǎn)生了極大的興趣：當(dāng)人們改變輸入特征時，機(jī)器學(xué)習(xí)模型的預(yù)測是如何改變的？

雖然一些可解釋的人工智能方法依賴于對數(shù)據(jù)進(jìn)行擾動以產(chǎn)生解釋[71, 72]，但是利用數(shù)據(jù)中自然發(fā)生的隨機(jī)性來估計因果效應(yīng)以保留原始數(shù)據(jù)的特征分布是有價值的，因?yàn)楫?dāng)給出一個分布不均勻的輸入數(shù)據(jù)時，機(jī)器學(xué)習(xí)模型可以表現(xiàn)得不符合常規(guī)[73]。結(jié)合準(zhǔn)實(shí)驗(yàn)和對他們的無偏因果估計，加上更靈活和更強(qiáng)大的機(jī)器學(xué)習(xí)方法，保證了這些方法能取長補(bǔ)短。

傳統(tǒng)的經(jīng)濟(jì)學(xué)工作更多地關(guān)注參數(shù)估計（例如，估計和解釋回歸系數(shù)）而非預(yù)測，這為機(jī)器學(xué)習(xí)融入準(zhǔn)實(shí)驗(yàn)方法帶來了機(jī)會[74]。在某些情況下，研究人員可以用更靈活的機(jī)器學(xué)習(xí)方法來代替?zhèn)鹘y(tǒng)方法中使用的參數(shù)估計。例如工具變量分析中的第一階段回歸實(shí)際上是一個預(yù)測任務(wù)。利用 LASSO 回歸、核方法和深度學(xué)習(xí)算法[75, 76, 77]，將工具變量擴(kuò)展到高維數(shù)據(jù)、非線性數(shù)據(jù)域。從時間序列數(shù)據(jù)推斷因果關(guān)系也越來越受到關(guān)注，在時間序列數(shù)據(jù)中，集合模型和矩陣填充（matirix completion）方法被用于因果估計[78, 79]。使用機(jī)器學(xué)習(xí)技術(shù)，結(jié)合時間序列中因果推斷，這一應(yīng)用方向前途光明。

另一個機(jī)器學(xué)習(xí)可以改進(jìn)準(zhǔn)實(shí)驗(yàn)的領(lǐng)域是精準(zhǔn)定位目標(biāo)人群來進(jìn)行因果估計。通過準(zhǔn)實(shí)驗(yàn)所作的估計只對特定群體有效——例如工具變量分析和斷點(diǎn)回歸中受某種工具或閾值影響的個人。預(yù)測哪些個體可能對某種干預(yù)或工具變量產(chǎn)生反應(yīng)[80, 81, 82]，可以增加因果估計的可解釋性，并為研究設(shè)計提供排除標(biāo)準(zhǔn)。此外，機(jī)器學(xué)習(xí)方法擅長優(yōu)化損失函數(shù)，這可以用于精準(zhǔn)干預(yù)策略的制定。例如，為了最大限度地發(fā)揮干預(yù)效果或最大限度地減少潛在危害[83, 84]，研究人員已經(jīng)開展了優(yōu)化斷點(diǎn)分析處理閾值的工作。機(jī)器學(xué)習(xí)擴(kuò)展后的準(zhǔn)實(shí)驗(yàn)方法可描述因果適用的目標(biāo)人群，為更好的政策選擇提供了信息。

實(shí)驗(yàn)經(jīng)濟(jì)學(xué)家對使用機(jī)器學(xué)習(xí)和數(shù)據(jù)科學(xué)很感興趣[74, 85, 86]。除了本文已經(jīng)回顧過的場景之外，還有其他場景下的因果推斷方法，例如在干擾下（個人的干預(yù)分配可能影響他人的結(jié)果）[87]，或者在網(wǎng)絡(luò)數(shù)據(jù)[88]中。隨著機(jī)器學(xué)習(xí)方法的普及，數(shù)據(jù)科學(xué)家和機(jī)器學(xué)習(xí)研究人員應(yīng)該尋找與經(jīng)濟(jì)學(xué)界合作的機(jī)會。

就像因果關(guān)系在營銷[89]和神經(jīng)科學(xué)[90]等領(lǐng)域被強(qiáng)調(diào)為中心問題一樣，人們需要更廣泛地認(rèn)識到，許多數(shù)據(jù)科學(xué)問題就是找到自然界中的因果關(guān)系[3]。研究人員提倡數(shù)據(jù)科學(xué)家通過一個因果透鏡來看待他們正在研究的問題: 這個問題是否能通過相關(guān)性或預(yù)測來回答，或者是否存在一個潛在的因果機(jī)制？如果目標(biāo)是了解決策、行動或干預(yù)，數(shù)據(jù)科學(xué)家需要仔細(xì)考慮他們的數(shù)據(jù)：這是觀察性的還是實(shí)驗(yàn)性的，是否存在對未觀察到的混雜變量，以及可以采取什么方法來控制混雜因子？準(zhǔn)實(shí)驗(yàn)是一套可以成功地識別混雜因果效應(yīng)的方法，其應(yīng)成為數(shù)據(jù)科學(xué)家工具包的一部分，就像它們已成為經(jīng)濟(jì)學(xué)家工具包的一部分一樣[49, 91]。

數(shù)據(jù)科學(xué)和準(zhǔn)實(shí)驗(yàn)的傳統(tǒng)用戶相互合作會帶來新的機(jī)會。因果關(guān)系需要在數(shù)據(jù)科學(xué)中發(fā)揮更大的作用，準(zhǔn)實(shí)驗(yàn)為從觀測數(shù)據(jù)中獲得的因果關(guān)系提供了實(shí)用的測量方法。與此同時，機(jī)器學(xué)習(xí)和數(shù)據(jù)科學(xué)的創(chuàng)新正在經(jīng)濟(jì)學(xué)中得到應(yīng)用，而這些思想在復(fù)雜數(shù)據(jù)領(lǐng)域的持續(xù)應(yīng)用可以擴(kuò)大經(jīng)濟(jì)學(xué)家和其他社會科學(xué)家可以提出問題的范圍。可以設(shè)想，在未來，更多的數(shù)據(jù)科學(xué)明確地圍繞著因果關(guān)系展開，其他領(lǐng)域如經(jīng)濟(jì)學(xué)可以利用機(jī)器學(xué)習(xí)的進(jìn)步來幫助回答他們自己的因果問題。

參考文獻(xiàn)

1. van Dyk, D. et al. ASA statement on the role of statistics in data science. Amstat News https://magazine.amstat.org/blog/2015/10/01/ asa-statement-on-the-role-of-statistics-in-data-science/ (2015).

2. Pearl, J. Te seven tools of causal inference, with refections on machine learning. Commun. ACM 62, 54–60 (2019).

3. Hernán, M. A., Hsu, J. & Healy, B. Data science is science’s second chance to get causal inference right: a classifcation of data science tasks. Chance 32, 42–49 (2019).

4. Caruana, R. et al. Intelligible models for healthcare: predicting pneumonia risk and hospital 30-day readmission. In Proc. 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 1721–1730 (ACM Press, 2015); https://doi.org/10.1145/2783258.2788613

5. Finkelstein, A. et al. Te Oregon health insurance experiment: evidence from the frst year. Q. J. Econ. 127, 1057–1106 (2012).

6. Forney, A., Pearl, J. & Bareinboim, E. Counterfactual data-fusion for online reinforcement learners. In International Conference on Machine Learning (eds. Precup, D. & Teh, Y. W.) 1156–1164 (PMLR, 2017).

7. Tomas, P. S. & Brunskill, E. Data-efcient of-policy policy evaluation for reinforcement learning. International Conference on Machine Learning (eds. Balcan, M. F. & Weinberger, K.) 2139–2148 (PMLR, 2016).

8. Athey, S. & Wager, S. Policy learning with observational data. Econometrica (in the press).

9. Angrist, J. D. & Pischke, J.-S. Mostly Harmless Econometrics: An Empiricist’s Companion (Princeton Univ. Press, 2008).

10. Imbens, G. & Rubin, D. B. Causal Inference: For Statistics, Social and Biomedical Sciences: An Introduction (Cambridge Univ. Press 2015).

11. Pearl, J. Causality (Cambridge Univ. Press, 2009).

12. Hernán, M. A. & Robins, J. M. Causal Inference: What If (Chapman & Hall/ CRC, 2020).

13. Pearl, J. Causal inference in statistics: an overview. Stat. Surv. 3, 96–146 (2009).

14. Peters, J., Janzing, D. & Sch?lkopf, B. Elements of Causal Inference: Foundations and Learning Algorithms (MIT Press, 2017).

15. Rosenbaum, P. R. & Rubin, D. B. Te central role of the propensity score in observational studies for causal efects. Biometrika 70, 41–55 (1983).

16. Chernozhukov, V. et al. Double/debiased machine learning for treatment and structural parameters. Econ. J. 21, C1–C68 (2018).

17. Spirtes, P., Glymour, C. N. & Scheines, R. Causation, Prediction, and Search (MIT Press, 2000).

18. Sch?lkopf, B. Causality for machine learning. Preprint at https://arxiv.org/ abs/1911.10500 (2019).

19. Mooij, J. M., Peters, J., Janzing, D., Zscheischler, J. & Sch?lkopf, B. Distinguishing cause from efect using observational data: methods and benchmarks. J. Mach. Learn. Res. 17, 1103–1204 (2016).

20. Huang, B. et al. Causal discovery from heterogeneous/nonstationary data. J. Mach. Learn. Res. 21, 1–53 (2020).

21. Wang, Y. & Blei, D. M. Te blessings of multiple causes. J. Am. Stat. Assoc. 114, 1574–1596 (2019).

22. Leamer, E. E. Let’s take the con out of econometrics. Am. Econ. Rev. 73, 31–43 (1983).

23. Angrist, J. D. & Pischke, J.-S. Te credibility revolution in empirical economics: how better research design is taking the con out of econometrics. J. Econ. Perspect.

24, 3–30 (2010). 24. Angrist, J. D. & Krueger, A. B. Instrumental variables and the search for identifcation: from supply and demand to natural experiments. J. Econ. Perspect. 15, 69–85 (2001).

25. Angrist, J. D. & Krueger, A. B. Does compulsory school attendance afect schooling and earnings? Q. J. Econ. 106, 979–1014 (1991).

26. Wooldridge, J. M. Econometric Analysis of Cross Section and Panel Data (MIT Press, 2010).

27. Angrist, J. D., Imbens, G. W. & Krueger, A. B. Jackknife instrumental variables estimation. J. Appl. Econom. 14, 57–67 (1999).

28. Newhouse, J. P. & McClellan, M. Econometrics in outcomes research: the use of instrumental variables. Annu. Rev. Public Health 19, 17–34 (1998).

29. Imbens, G. Potential Outcome and Directed Acyclic Graph Approaches to Causality: Relevance for Empirical Practice in Economics Working Paper No. 26104 (NBER, 2019); https://doi.org/10.3386/w26104

30. Hanandita, W. & Tampubolon, G. Does poverty reduce mental health? An instrumental variable analysis. Soc. Sci. Med. 113, 59–67 (2014).

31. Angrist, J. D., Graddy, K. & Imbens, G. W. Te interpretation of instrumental variables estimators in simultaneous equations models with an application to the demand for fsh. Rev. Econ. Stud. 67, 499–527 (2000).

32. Tistlethwaite, D. L. & Campbell, D. T. Regression-discontinuity analysis: an alternative to the ex post facto experiment. J. Educ. Psychol. 51, 309–317 (1960).

33. Fine, M. J. et al. A prediction rule to identify low-risk patients with community-acquired pneumonia. N. Engl. J. Med. 336, 243–250 (1997).

34. Lee, D. S. & Lemieux, T. Regression discontinuity designs in economics. J. Econ. Lit. 48, 281–355 (2010).

35. Cattaneo, M. D., Idrobo, N. & Titiunik, R. A Practical Introduction to Regression Discontinuity Designs (Cambridge Univ. Press, 2019).

36. Imbens, G. & Kalyanaraman, K. Optimal Bandwidth Choice for the Regression Discontinuity Estimator Working Paper No. 14726 (NBER, 2009); https://doi. org/10.3386/w14726

37. Calonico, S., Cattaneo, M. D. & Titiunik, R. Robust data-driven inference in the regression-discontinuity design. Stata J. 14, 909–946 (2014).

38. McCrary, J. Manipulation of the running variable in the regression discontinuity design: a density test. J. Econ. 142, 698–714 (2008).

39. Imbens, G. & Lemieux, T. Regression discontinuity designs: a guide to practice. J. Economet. 142, 615–635 (2008).

40. NCI funding policy for RPG awards. NIH: National Cancer Institute https://deainfo.nci.nih.gov/grantspolicies/fnalfundltr.htm (2020).

41. NIAID paylines. NIH: National Institute of Allergy and Infectious Diseases http://www.niaid.nih.gov/grants-contracts/niaid-paylines (2020).

42. Keele, L. J. & Titiunik, R. Geographic boundaries as regression discontinuities. Polit. Anal. 23, 127–155 (2015).

43. Card, D. & Krueger, A. B. Minimum Wages and Employment: A Case Study of the Fast Food Industry in New Jersey and Pennsylvania Working Paper No. 4509 (NBER, 1993); https://doi.org/10.3386/w4509

44. Ashenfelter, O. & Card, D. Using the Longitudinal Structure of Earnings to Estimate the Efect of Training Programs Working Paper No. 1489 (NBER, 1984); https://doi.org/10.3386/w1489

45. Angrist, J. D. & Krueger, A. B. in Handbook of Labor Economics Vol. 3 (eds. Ashenfelter, O. C. & Card, D.) 1277–1366 (Elsevier, 1999).

46. Athey, S. & Imbens, G. W. Identifcation and inference in nonlinear diference-in-diferences models. Econometrica 74, 431–497 (2006).

47. Abadie, A. Semiparametric diference-in-diferences estimators. Rev. Econ. Stud. 72, 1–19 (2005).

48. Lu, C., Nie, X. & Wager, S. Robust nonparametric diference-in-diferences estimation. Preprint at https://arxiv.org/abs/1905.11622 (2019).

49. Besley, T. & Case, A. Unnatural experiments? estimating the incidence of endogenous policies. Econ. J. 110, 672–694 (2000).

50. Nunn, N. & Qian, N. US food aid and civil confict. Am. Econ. Rev. 104, 1630–1666 (2014).

51. Christian, P. & Barrett, C. B. Revisiting the Efect of Food Aid on Confict: A Methodological Caution (Te World Bank, 2017); https://doi. org/10.1596/1813-9450-8171.

52. Angrist, J. & Imbens, G. Identifcation and Estimation of Local Average Treatment Efects Technical Working Paper No. 118 (NBER, 1995); https://doi.org/10.3386/t0118

53. Hahn, J., Todd, P. & Van der Klaauw, W. Identifcation and estimation of treatment efects with a regression-discontinuity design. Econometrica 69, 201–209 (2001).

54. Angrist, J. & Rokkanen, M. Wanna Get Away? RD Identifcation Away from the Cutof Working Paper No. 18662 (NBER, 2012); https://doi.org/10.3386/ w18662

55. Rothwell, P. M. External validity of randomised controlled trials: “To whom do the results of this trial apply?”. Te Lancet 365, 82–93 (2005).

56. Rubin, D. B. For objective causal inference, design trumps analysis. Ann. Appl. Stat. 2, 808–840 (2008).

57. Chaney, A. J. B., Stewart, B. M. & Engelhardt, B. E. How algorithmic confounding in recommendation systems increases homogeneity and decreases utility. In Proc. 12th ACM Conference on Recommender Systems 224–232 (Association for Computing Machinery, 2018); https://doi. org/10.1145/3240323.3240370.

58. Sharma, A., Hofman, J. M. & Watts, D. J. Estimating the causal impact of recommendation systems from observational data. In Proc. Sixteenth ACM Conference on Economics and Computation 453–470 (Association for Computing Machinery, 2015); https://doi.org/10.1145/2764468.2764488

59. Lawlor, D. A., Harbord, R. M., Sterne, J. A. C., Timpson, N. & Smith, G. D. Mendelian randomization: using genes as instruments for making causal inferences in epidemiology. Stat. Med. 27, 1133–1163 (2008).

60. Zhao, Q., Chen, Y., Wang, J. & Small, D. S. Powerful three-sample genome-wide design and robust statistical inference in summary-data Mendelian randomization. Int. J. Epidemiol. 48, 1478–1492 (2019).

61. Moscoe, E., Bor, J. & B?rnighausen, T. Regression discontinuity designs are underutilized in medicine, epidemiology, and public health: a review of current and best practice. J. Clin. Epidemiol. 68, 132–143 (2015).

62. Blake, T., Nosko, C. & Tadelis, S. Consumer heterogeneity and paid search efectiveness: a large-scale feld experiment. Econometrica 83, 155–174 (2015).

63. Dimick, J. B. & Ryan, A. M. Methods for evaluating changes in health care policy: the diference-in-diferences approach. JAMA 312, 2401–2402 (2014).

64. Kallus, N., Puli, A. M. & Shalit, U. Removing hidden confounding by experimental grounding. Adv. Neural Inf. Process. Syst. 31, 10888–10897 (2018).

65. Zhang, J. & Bareinboim, E. Markov Decision Processes with Unobserved Confounders: A Causal Approach. Technical Report (R-23) (Columbia CausalAI Laboratory, 2016).

66. Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).

67. Lansdell, B., Triantafllou, S. & Kording, K. Rarely-switching linear bandits: optimization of causal efects for the real world. Preprint at https://arxiv.org/ abs/1905.13121 (2019).

68. Adadi, A. & Berrada, M. Peeking inside the black-box: a survey on explainable artifcial intelligence (XAI). IEEE Access 6, 52138–52160 (2018).

69. Zhao, Q. & Hastie, T. Causal interpretations of black-box models. J. Bus. Econ. Stat. 39, 272–281 (2021).

70. Morafah, R., Karami, M., Guo, R., Raglin, A. & Liu, H. Causal interpretability for machine learning—problems, methods and evaluation. ACM SIGKDD Explor. Newsl. 22, 18–33 (2020).

71. Ribeiro, M. T., Singh, S. & Guestrin, C. ‘Why should I trust you?’: Explaining the predictions of any classifer. In Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 1135–1144 (Association for Computing Machinery, 2016); https://doi.org/10.1145/2939672.2939778

72. Mothilal, R. K., Sharma, A. & Tan, C. Explaining machine learning classifers through diverse counterfactual explanations. In Proc. 2020 Conference on Fairness, Accountability, and Transparency 607–617 (Association for Computing Machinery, 2020); https://doi.org/10.1145/3351095.3372850

73. Hooker, G. & Mentch, L. Please stop permuting features: an explanation and alternatives. Preprint at https://arxiv.org/abs/1905.03151 (2019).

74. Mullainathan, S. & Spiess, J. Machine learning: an applied econometric approach. J. Econ. Perspect. 31, 87–106 (2017).

75. Belloni, A., Chen, D., Chernozhukov, V. & Hansen, C. Sparse models and methods for optimal instruments with an application to eminent domain. Econometrica 80, 2369–2429 (2012).

76. Singh, R., Sahani, M. & Gretton, A. Kernel instrumental variable regression. Adv. Neural Inf. Process. Syst. 32, 4593–4605 (2019).

77. Hartford, J., Lewis, G., Leyton-Brown, K. & Taddy, M. Deep IV: a fexible approach for counterfactual prediction. In Proc. 34th International Conference on Machine Learning Vol. 70 (eds. Precup, D. & Teh Y. W.) 1414–1423 (JMLR.org, 2017).

78. Athey, S., Bayati, M., Doudchenko, N., Imbens, G. & Khosravi, K. Matrix Completion Methods for Causal Panel Data Models Working Paper No. 25132 (NBER, 2018); https://doi.org/10.3386/w25132

79. Athey, S., Bayati, M., Imbens, G. & Qu, Z. Ensemble methods for causal efects in panel data settings. AEA Pap. Proc. 109, 65–70 (2019).

80. Kennedy, E. H., Balakrishnan, S. & G’Sell, M. Sharp instruments for classifying compliers and generalizing causal efects. Ann. Stat. 48, 2008–2030 (2020).

81. Kallus, N. Classifying treatment responders under causal efect monotonicity. In Proc. 36th International Conference on Machine Learning Vol. 97 (eds. Chaudhuri, K. & Salakhutdniov, R.) 3201–3210 (PMLR, 2019).

82. Li, A. & Pearl, J. Unit selection based on counterfactual logic. In Proc. Twenty-Eighth International Joint Conference on Artifcial Intelligence (ed. Kraus, S.) 1793–1799 (International Joint Conferences on Artifcial Intelligence Organization, 2019); https://doi.org/10.24963/ijcai.2019/248

83. Dong, Y. & Lewbel, A. Identifying the efect of changing the policy threshold in regression discontinuity models. Rev. Econ. Stat. 97, 1081–1092 (2015).

84. Marinescu, I. E., Triantafllou, S. & Kording, K. Regression discontinuity threshold optimization. SSRN https://doi.org/10.2139/ssrn.3333334 (2019).

85. Varian, H. R. Big data: new tricks for econometrics. J. Econ. Perspect. 28, 3–28 (2014).

86. Athey, S. & Imbens, G. W. Machine learning methods that economists should know about. Annu. Rev. Econ. 11, 685–725 (2019).

87. Hudgens, M. G. & Halloran, M. E. Toward causal inference with interference. J. Am. Stat. Assoc. 103, 832–842 (2008).

88. Graham, B. & de Paula, A. Te Econometric Analysis of Network Data (Elsevier, 2019).

89. Varian, H. R. Causal inference in economics and marketing. Proc. Natl. Acad. Sci. USA 113, 7310–7315 (2016).

90. Marinescu, I. E., Lawlor, P. N. & Kording, K. P. Quasi-experimental causality in neuroscience and behavioural research. Nat. Hum. Behav. 2, 891–898 (2018).

91. Abadie, A. & Cattaneo, M. D. Econometric methods for program evaluation. Annu. Rev. Econ. 10, 465–503 (2018).

（參考文獻(xiàn)可上下滑動查看）

因果科學(xué)第二季讀書會報名中

因果推斷與機(jī)器學(xué)習(xí)領(lǐng)域的結(jié)合已經(jīng)吸引了越來越多來自學(xué)界業(yè)界的關(guān)注，為深入探討、普及推廣因果科學(xué)議題，幫助其他領(lǐng)域如經(jīng)濟(jì)學(xué)可以利用機(jī)器學(xué)習(xí)的進(jìn)步來幫助回答他們自己的因果問題，集智俱樂部攜手智源社區(qū)將舉辦第二季「」。本期讀書會著力于實(shí)操性、基礎(chǔ)性，將帶領(lǐng)大家精讀因果科學(xué)方向兩本非常受廣泛認(rèn)可的入門教材。

1. Pearl, Judea, Madelyn Glymour, and Nicholas P. Jewell. Causal inference in statistics: A primer. John Wiley & Sons, 2016.（本書中譯版《統(tǒng)計因果推理入門（翻譯版）》已由高等教育出版社出版）

2. Peters, Jonas, Dominik Janzing, and Bernhard Sch?lkopf. Elements of causal inference: foundations and learning algorithms. The MIT Press, 2017.

讀書會每周將進(jìn)行直播討論，進(jìn)行問題交流、重點(diǎn)概念分享、閱讀概覽和編程實(shí)踐內(nèi)容分析。非常適合有機(jī)器學(xué)習(xí)背景，希望深入學(xué)習(xí)因果科學(xué)基礎(chǔ)知識和重要模型方法，尋求解決相關(guān)研究問題的朋友參加。

目前因果科學(xué)讀書會系列，已經(jīng)有接近400多位的海內(nèi)外高校科研院所的一線科研工作者以及互聯(lián)網(wǎng)一線從業(yè)人員參與，吸引了國內(nèi)和國際上大部分的因果科學(xué)領(lǐng)域的專業(yè)科研人員，如果你也對這個主題感興趣，想要深度地參與，就快加入我們吧！

詳情請點(diǎn)擊：

報名：（長期有效）

第一步：掃碼填寫報名信息。

第二步：信息填寫之后，進(jìn)入付款流程，提交保證金299元。（符合退費(fèi)條件后可退費(fèi)。）

第三步：添加負(fù)責(zé)人微信，拉入對應(yīng)的讀書會討論群。

我們也會對每次分享的內(nèi)容進(jìn)行錄制，剪輯后發(fā)布在集智學(xué)園的官網(wǎng)上，供讀書會成員回看。

因果科學(xué)讀書會第二季第一期將在周日（3月21日）上午10:00開展，我們將和大家一起來建立對因果科學(xué)的全局認(rèn)知，系統(tǒng)了解因果推斷，從而打好基礎(chǔ)，在接下來的讀書會內(nèi)容學(xué)習(xí)中起到事半功倍的效果。

本次分享邀請了英國劍橋大學(xué)機(jī)器學(xué)習(xí)組博士生陸超超來進(jìn)行分享，他將從以下幾個方面跟大家展開深度的討論：

1. 講述因果推斷的兩大框架：潛在結(jié)果模型和結(jié)構(gòu)因果模型，討論他們各自的優(yōu)缺點(diǎn)以及他們之間的聯(lián)系，詳細(xì)介紹他們之間的轉(zhuǎn)化規(guī)律。

2. 與大家一起深入探討因果推斷中最基本的概念、定理以及它們產(chǎn)生的緣由，了解每個概念背后的故事，從而建立起對因果更全面的感知。

3. 分享它們在不同學(xué)科中的具體的應(yīng)用，包括社會科學(xué)、經(jīng)濟(jì)學(xué)、醫(yī)學(xué)、機(jī)器學(xué)習(xí)等，借助這些應(yīng)用，進(jìn)一步啟發(fā)大家用因果科學(xué)思維來思考和解決問題。

原標(biāo)題：《Nature計算科學(xué)綜述：經(jīng)由準(zhǔn)實(shí)驗(yàn)，從觀察數(shù)據(jù)中推測因果關(guān)系》

閱讀原文