原創 扈鴻業 集智俱樂部

導語

深度學習技術，尤其是生成模型在圖像問題處理上大放異彩。 而生成模型之所以展現出強大的多層信號處理能力，與物理學中的重整化群理論密切相關。研究者結合重整化群方法和流模型，開發出可以發現自然作用力的AI“物理學家”，以及具有高可解釋性與可控性的計算機視覺生成模型。相關研究發表在 Physical Review Research、Physical Review Letters 等期刊上，本文是對該研究方向的介紹。

本文作者、加州大學圣地亞哥分校博士生扈鴻業是集智凱風獎學金獲得者。

扈鴻業 | 作者

鄧一雪 | 編輯

第零部分 序

隨著深度學習的發展，我們已經感受到了機器學習在計算機視覺、自然語言處理、強化學習等諸多領域取得了令人贊嘆的進展，這些先進的技術也在隨著時間的推移進入人類的生活，幫助人類優化其生產力。作為一個新興的學科與技術，深度學習也在科學研究上嶄露頭角。一方面，大家把深度學習、神經網絡作為一個獨立的客體，試圖理解它的行為，并借助人類已知的一些概念設計更有趣的神經網絡；另一方面，神經網絡也作為一個新型的工具幫助科學家通過更快的模擬量子物理、量子化學，挖掘生物信息等等來理解自然世界。

第一部分 基于流模型的生成模型

在深度學習中一類重要的問題叫做生成模型（generative model）。比如我們擁有如下圖的人臉數據集，我們如何生成更多類似的人臉數據并且讓生成的數據看起來和真的一樣呢？生成模型想解決的就是這個問題，比如圖1中有很多人像照片，他們是由真實人類通過照相攝影產生的。那么圖2中也有四張人像照片，你是不是很難分辨這四個人哪個是真實的人類，而哪個是機器產生的“假人類”呢？實際上這四張圖片都是由作者在撰寫此稿的時候機器想象出來的假人，不知道你答對了嘛？

圖1

圖2

生成模型具體實現的方式有很多，比如生成對抗網絡（generative adversarial networks）、變分自動編碼器（variational autoencoder）、流模型（flow-based model）等等。本文將主要關注在流模型上（具體說是連續空間的流模型，即

的取值范圍是實數域）。簡單來說，流模型就是通過一系列的可逆變換把一張容易得到的白噪聲圖片變換成一個我們想要的圖片的工具。如圖3所示，通過對像素的變換可以把一張白噪聲圖片轉換成一張小女孩的照片。更形象一些，我們可以把流模型想象成一雙神奇的藝術家之手，經過這雙神奇的手我們可以把散漫無序的沙堆砌成我們想要的藝術品，那么如何找到這樣一雙神奇之手呢？我們將采取神經網絡來對它建模。

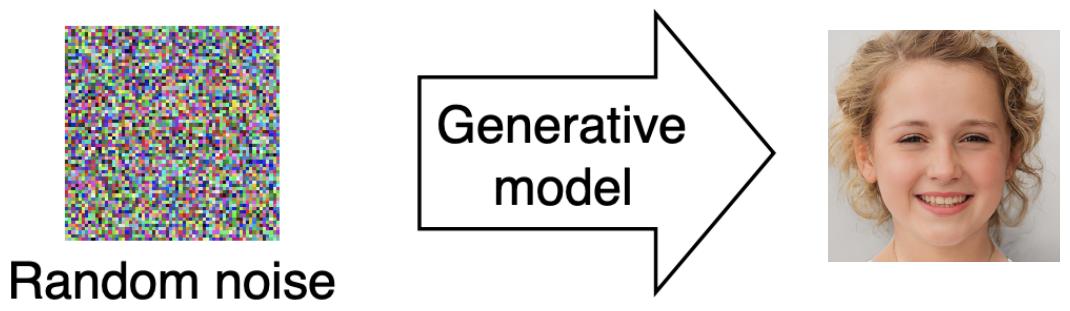
圖3

從數學上去理解生成模型在做什么，我們可以認為這些真實的人臉數據都是從某一個我們并不知道的概率密度分布中采樣出來的，其中就是每一張圖片。這樣看來，讓一個機器去生成更多長得像“真人”一樣的圖片，從數學上就變成了讓機器產生一個變分概率去擬合真實的人臉分布。如果機器可以擬合得足夠好，那么我們就可以從產生更多的圖片，他們也會很像真實的人臉。

為了更好地理解流模型，我們先來看一個簡單的例子。假設我們有一個紅色的雙峰概率密度分布 p(x) ，如圖4所示，我們如何從這個分布里面去進行采樣呢？

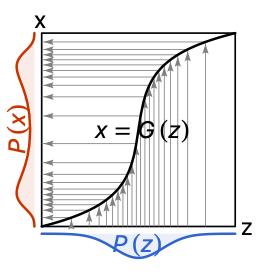
圖4

假設我們可以從高斯分布中做直接的采樣，即我們可以從藍色的 p(z) 分布進行對的直接采樣，那么我們可以找到一個可逆的雙射（bijective map），x=G(z) ，把每一個 z 映射到 x。我們可以看到這個映射G在中間導數很大，兩邊導數很小，這樣就可以在映射之后中間的部分采樣稀疏，而兩邊的地方采樣密集。這樣我們就可以對高斯分布進行直接采樣，然后把得到的z按照雙射變換為x，從而實現對x的直接采樣。數學上這樣兩個分布有如下的聯系：

其中被稱作雅克比行列式。如此看來，我們想去對一個復雜的概率密度分布采樣，如果可以找到這樣一個雙射，把這個復雜的分布變成簡單的分布，比如高斯分布，我們便能對復雜的分布進行直接采樣。那么我們要如何去尋找這樣一個雙射呢？一個想法是我們去構造一個變分假設，其中θ泛指變分假設中所有的參數。通過這個變分假設的雙射，我們可以把簡單的分布變換成現在我們想去對變分參數θ進行優化，使得盡可能的逼近目標概率密度分布。對于兩個概率密度分布的“距離”，其中一個常用的指標是KL散度（Kullback-Leibler divergence），它的定義是KL散度可以證明是一個大于等于0的量，當兩個概率密度完全一致的時候，KL散度為0。所以通常我們可以去優化減小變分分布和目標分布的KL散度，使得他們更加相近。（注：但是KL散度不是嚴格意義上的距離，因為p和q不具備交換對稱性）

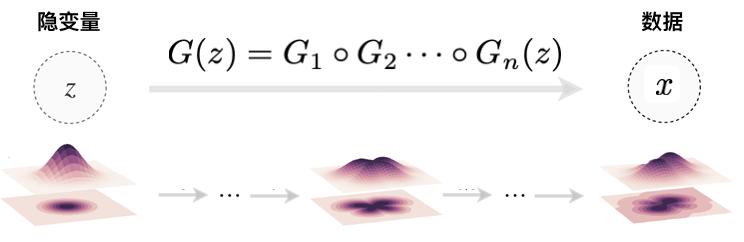
圖5

那么我們要如何去構造一個足夠一般的雙射變換作為變分假設使得它可以盡可能去擬合任意的可逆變換（雙射）呢？根據深度學習的思想，我們可以構造一些相對簡單的雙射 Gi ，然后把他們如圖5所示一樣的串聯起來，從而形成一個相對復雜的變分假設。這樣的想法就和搭建樂高積木一樣，我們希望構造一些樂高積木的基本單元，然后通過迭代讓他們涌現出復雜的行為。這點和凝聚態物理中簡單的粒子通過相互作用來涌現復雜的行為也有異曲同工之妙。在機器學習的研究中，人們提出了一些基本的可逆變換，被大家廣泛使用，比如Real NVP、invertible convolution、invertible resnet等等。如何構造表達能力強且簡單的可逆變換，也是生成型模型研究的一個重點。而我們本文想要討論的是假設我們已經擁有了基本的可逆變換作為樂高積木的話，我們應該按照什么樣子的藍圖來搭建它們，使得他們組成一個”智能“的網絡能處理具有多層次特點的自然信號呢？

第二部分 重整化群流模型與全息原理

為了更好地理解生成型模型和物理學的關系，先讓我們來看一看（量子）場論是如何與計算機科學中的圖片集構建聯系的。物理學中的場（field）是對時空的連續性描述，可以把它看做是時空到某一個流形（manifold）的映射。通俗一點講，我們可以舉一個例子。如圖6所示，我們可以把一個二維時空的標量場（scalar field）看做是一張灰度圖，即每一個像素點被映射到一個標量上；而二維時空的矢量場可以被類比為一張RGB彩色圖片，每個像素有一個RGB矢量來表示顏色。這樣我們就可以把物理中場論中場的各種構型看成一張張不同的圖片。那么我們怎么通俗地理解場論呢？

圖6

場論給每一個場的構型設定了一個概率或者negative log-likelihood，就如圖7所示。那么有的場的構型出現的概率較大，有的場構型出現的概率較小。這就類似于人臉圖片集中人臉出現的概率就比白噪聲出現的次數要多得多。如此看來，大自然本身就是一個生成模型，它無時無刻不在為我們生成和展現它自己美麗的圖片。而從這個角度來看，人工智能中的生成型模型也是對場論的一個很自然的描述。所以我們自然會想知道如何可以構建一個人工智能的生成模型來描述場論，描述自然。當我們給這個AI一個場論的描述（action）之后，它是不是能學習出物理，然后像大自然一樣為我們生成符合這個場論描述的場構型呢？

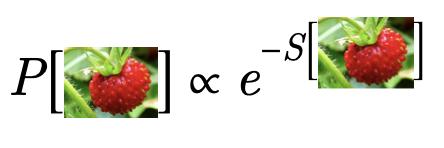
圖7

大自然中的信號是分尺度的。在每個尺度都涌現出了不同的有效理論，就如圖8中這個蛇形圖案給我們展現一樣。在微觀尺度我們具有量子力學、粒子物理學。如果我們把觀察的尺度再放大一些，我們就會有化學、生物學等等。凝聚態物理學大師 P. W. Anderson 先生在70年代撰寫過一篇名為“more is different”的文章。文中向大家闡述了隨著體系中客體數量的增加，由于多個客體間的相互作用，整體可能涌現出復雜的行為，并且這些行為是單個客體所不具備的。這也是為什么不同尺度會涌現出不同的理論的一個原因。那么有沒有一個理論可以作為橋梁來鏈接不同尺度的理論呢？在物理學中，這樣的理論叫做重整化群（renormalization group）。

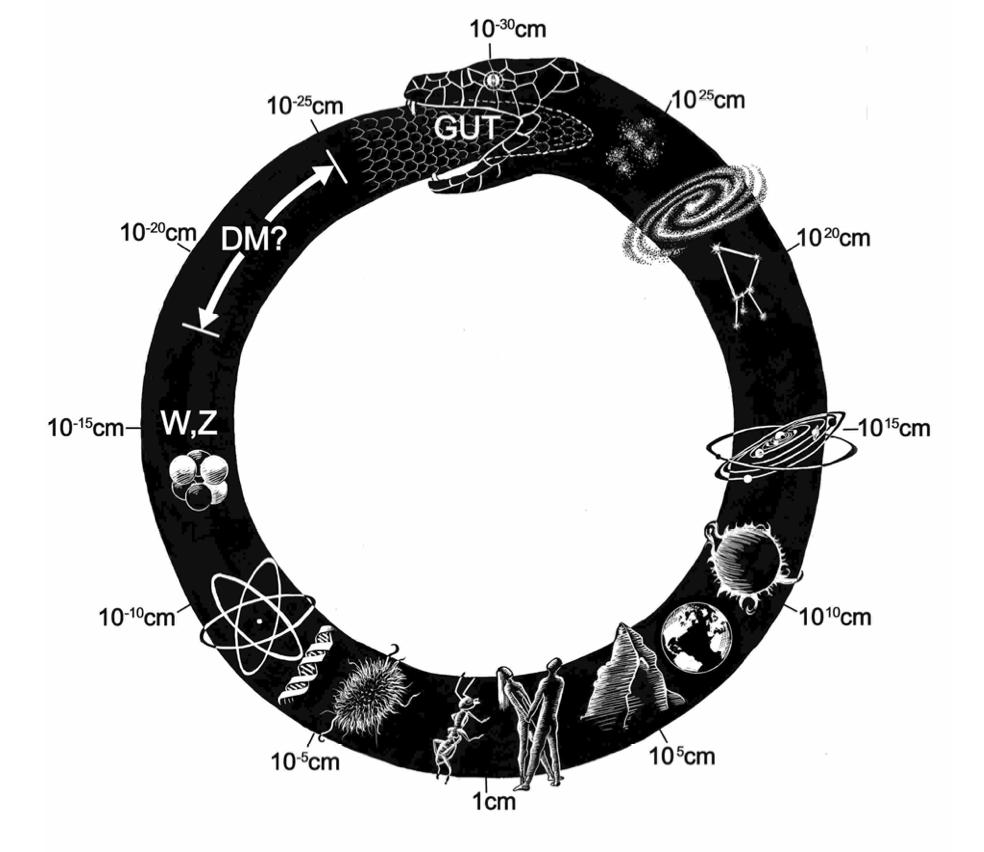
圖8

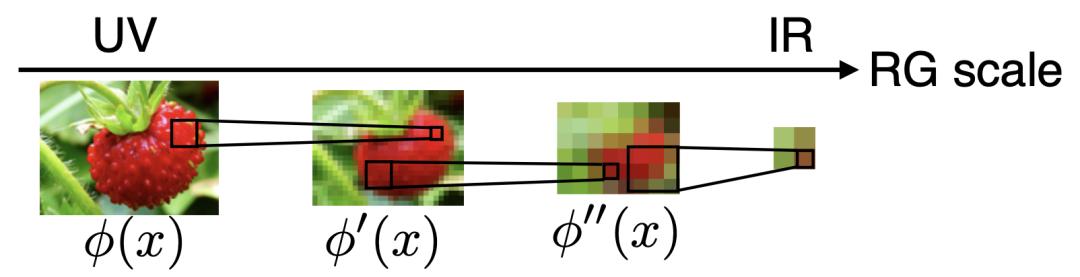
圖9

簡單來說，我們可以把重整化群的操作想象成對圖片不斷進行局部粗粒化的操作，從而我們對于體系的描述也從微觀（UV）變得越來越宏觀（IR），通過不斷的抹去細節不重要的信息，我們得到的是對體系更加重要的宏觀信息。這個過程也可以用圖9的卡通來進行展示。當然，對于傳統的物理體系，局部粗粒化的規則是物理學家通過對物理體系的分析和人類的智慧來定義的。自然我們也會想到，如果生成型模型AI是大自然的一個假設（ansatz)，那么它能不能也自己定義局部粗粒化的規則，來分析出體系中哪些信號是局部的，而哪些信號是宏觀的呢？通過對這些問題的思考，我們一同提出了重整化群的流模型和重整化群的信息學理論。

首先，我們看到了在傳統意義重整化群粗粒化的過程下，局部信息是被丟棄掉了。這樣具有局部信息損失而造成了傳統意義下的重整化群操作是不可逆的。所以我們擴展了重整化群的操作，與其在局部粗粒化的過程中抹去不重要的細節信息，我們可以不去丟掉它，而是把它留下來放到一個“容器”中存著它。這樣如果我們想從大尺度的圖片出發，反向還原細節圖片的話我們就可以再一次把“容器”中留下的這些信息片段補回去，就如圖10所示。（關于網絡更多的細節歡迎閱讀我們的文章，或聯系作者）

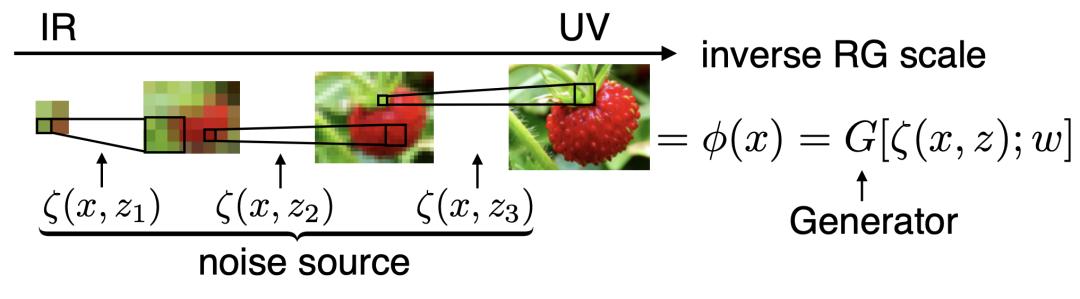
圖10

圖11

我們設計了具有多層級局部操作的神經網絡（圖11）。但是如何保證這些局部操作完成的是重整化群操作呢？為此我們在文章中也討論了重整化群的信息學理論，可以簡單地理解為機器需要把局部操作中丟到“容器”中保存下來不重要的東西盡可能像白噪聲。通過這樣的信息學指導和具有多層級局部操作的神經網絡結構，我們的“人工物理學家”已經搭建完備了！為了檢測它是不是具有分析物理體系性質，和生成物理體系構型的能力，我們拿物理中complex phi-4場論來對它進行了測試。

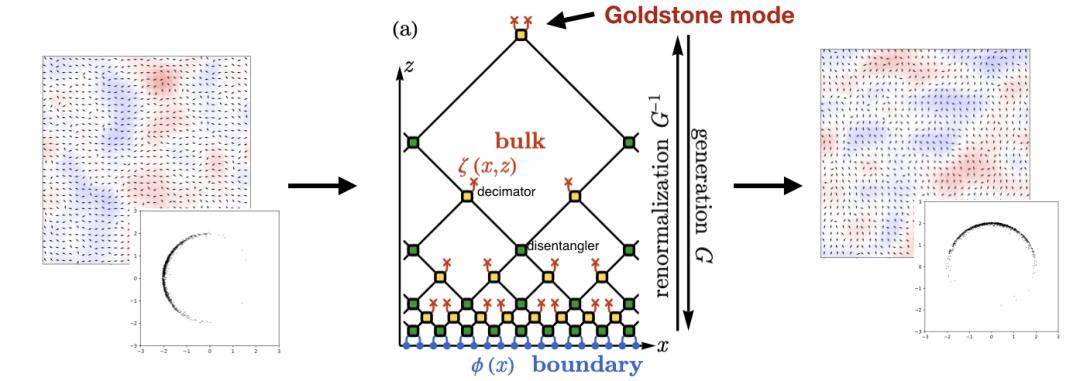
圖12

它在一定極限下的簡易模型可以理解為在一個二維網格上每個節點放置一個小磁針。小磁針在一定溫度下由于熱漲落希望在格點上隨意轉圈。而小磁針之間也會有相互作用力，它們喜歡一致，而不喜歡“異類”。也就是說它們都指向同一個方向會讓他們能量更低，更舒服。這樣一個簡單的體系具有豐富的物理內容，人們發現在一定溫度的時候體系會發生一個相變。在低溫的時候小磁針都會彼此順著對方進行整體的旋轉，而在高溫的時候他們就會完全無序的各自隨意旋轉。這個相變也是2016年諾貝爾物理學獎的重要工作之一。圖13卡通展示了小磁針模型的一個場構型。

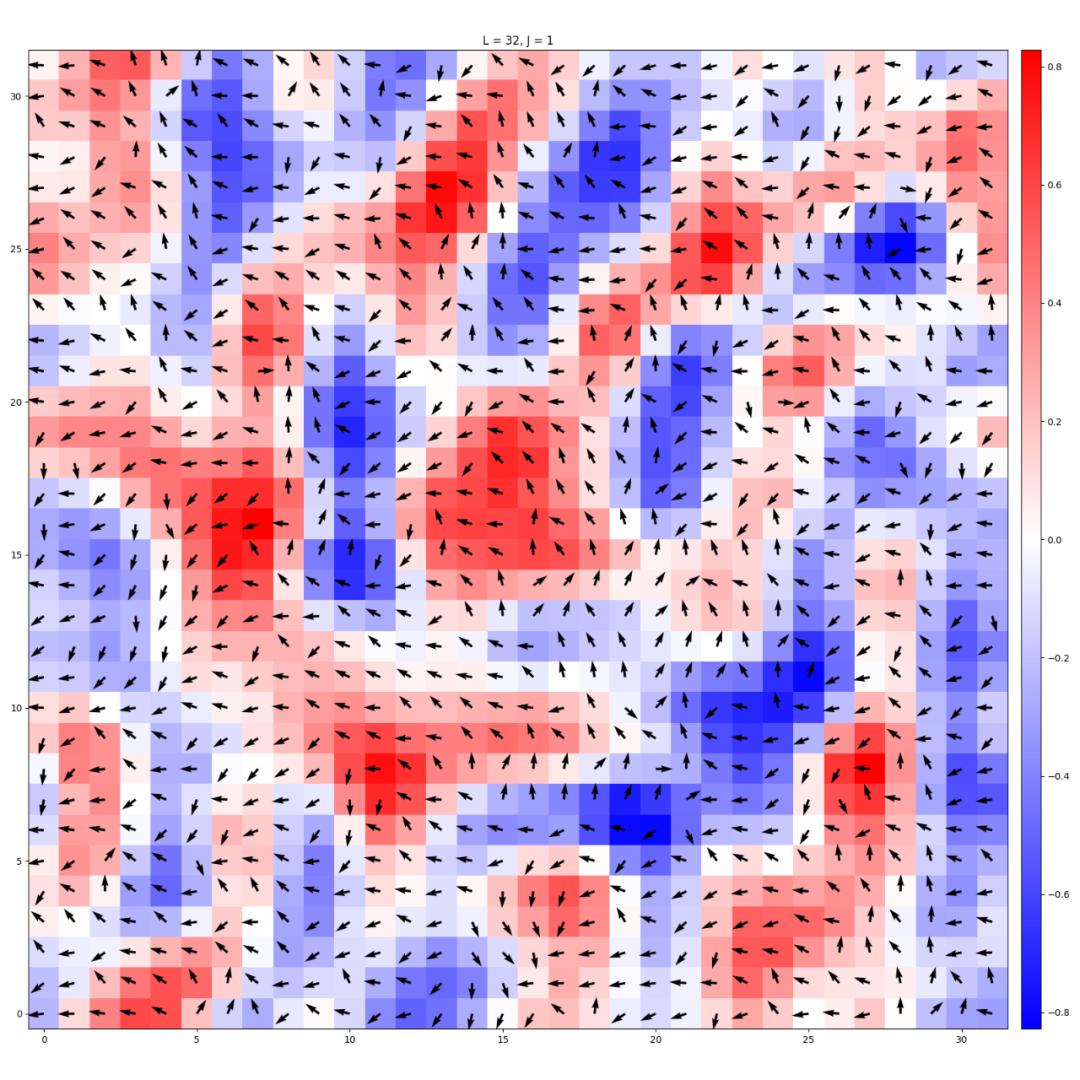
圖13

現在我們給了機器對于這個體系最為精簡的描述，即能量函數，它是不是能發現這些有趣的物理呢？我們發現對于不同的溫度，這個AI確實可以發現這個體系具有兩個行為不同的區間，更為準確地說是兩個不同的相（phase）。

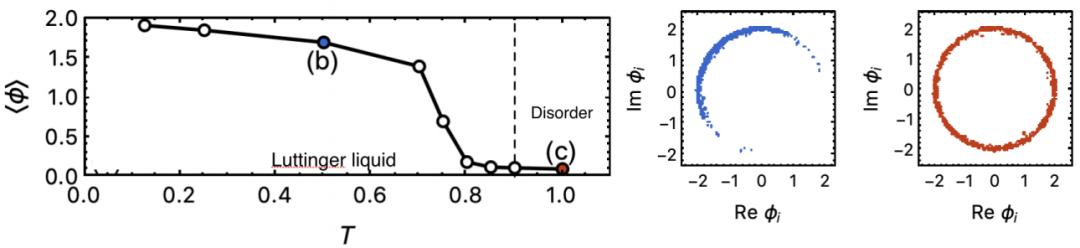
圖14

如圖14所示，機器可以通過計算發現在低溫的時候體系是在拉廷格液體相，而在高溫的時候體系在無序相，更準確的機器可以計算出在不同區間關聯函數行為的不同。這說明我們的構架的AI可以通過能量函數來學習到一些有趣的物理。并且我們的AI在設計的時候就希望它能夠自發地分析和區分大尺度低能的物理自由度和小尺度高能的物理自由度，我們也在實驗中驚喜地發現在網絡上端描述大尺度的地方，它找到了對于這個體系低能的goldstone mode。 （注：理論上此二維體系沒有對稱性自發破缺，所以不應該有goldstone mode，但是對于有限尺度體系，體系大小會造成對稱性破缺，所以有對應的goldstone mode）

那么構建一個這樣的AI“物理學家”有什么用呢？首先，我們看到了它可以根據體系的最精簡描述來發現體系不同的相，并且它能夠區分出什么是局部細節信息和宏觀的大尺度信息。而且作為一個生成型模型，它一旦學習完備，就可以像大自然一樣很快地幫我們產生對于這個體系大量的圖片（snapshot），幫助我們快速有效地數值模擬這個物理體系。看到這里，不知道你是不是覺得這個很神奇呢？下面我們介紹一些更加神奇而有趣的物理。

我們都知道大自然有四種基本的相互作用：1. 萬物都有的萬有引力；2. 掌控電磁的電磁力；3. 小尺度上的弱相互作用；4. 最強王者強相互作用。那么除了第一種力之外我們對剩下三個力都有了量子理論的描述，統一被稱為標準模型（standard model）。對于引力，我們對它只有經典描述，沒有量子描述。那么，引力究竟是什么？在過去的很長時間里吸引了大量的物理學家對其進行研究。從愛因斯坦的理論中，我們學習到了引力可以被理解成一種時空的扭曲，一種時空的幾何性質。在21世紀初，物理學家胡安（Juan Maldacena）做出了另一個令大家興奮的發現，就是某一些特定的量子理論可以看做是一個經典引力理論的邊界，它們嚴格對應，是對同一種物體的兩種不同描述。這樣的理論我們可以科幻地想象成“瓶中宇宙”（如圖15所示）。在瓶子的邊緣上生活著量子理論，它可能是二維的，那么它對應于瓶子里面就存在著一個三維的宇宙，具有經典的引力。這樣的事情就像看3D電影一樣，銀幕上是一個二維的平面，但是一旦你帶上了3D眼鏡，就觀察到了3D的“新世界”。而這個3D世界上所有的信息其實都包含在這個二維銀幕上。

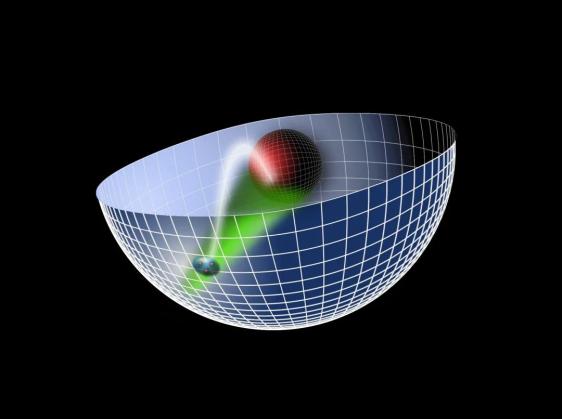
圖15

那么我們給機器生活在二維“銀幕”上的量子體系，它能不能發現這個銀幕背后描述的3D世界發生的五彩繽紛的故事呢？我們用重整化群流模型這個人工智能對此進行了測試，提供給它”瓶子“邊界上的量子體系，經過學習二維的量子體系，我們發現它的三維體空間確實存在一個有序的幾何結構，也就是引力體系，就如圖16(b)中展示的一樣，非常漂亮。（注：更多嚴謹描述見論文）

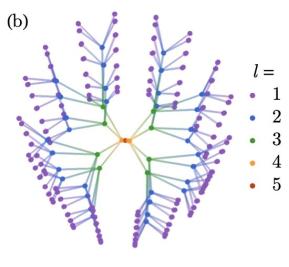
圖16

最后借用王磊老師的一句話進行本章的結尾：

“如果物理學家是把咖啡變成公式的’機器’，那么生成模型就是把公式再變成我們看到的五彩繽紛大自然的智能。”

第三部分 重整化群流模型與計算機視覺

上面我們介紹了重整化群流模型在物理學中的一些應用，通過它來模擬物理體系、區分小尺度和大尺度的信號、解碼全息宇宙等等。下面我們來看一看這個物理學家們研發的AI在其他任務上有沒有什么應用價值呢？

圖17

大自然中的眾多的信號都是具有多層級結構的，這就啟發我們去探索應用同樣的思想是不是能夠構建一個神經網絡來處理自然圖片。就拿圖17的人臉圖片舉個例子，一張人臉的圖片，在大尺度下能提供給我們的信息是這個人的性別、年齡、情感（比如是不是開心）等等，在中等尺度上的信息可能是眼睛大小、鼻梁高低、有沒有發簾等等，在更細小的尺度上提供給我們的可能是臉上皺紋的紋理、胡須等等。這些都是蘊含在一張人臉圖片中不同尺度上的信息。人工智能在生成“虛擬”人臉、“虛擬”視頻上已經做到了爐火純青的地步，值得一提的是，上面五張人臉都是由機器自主生成的，我們很難看出來它和一個真正的人的照片的區別（所以可能也沒有版權的問題）。但是僅僅是生成很漂亮的圖片還沒有到達真正的智能。為了更近一步，我們希望這個機器在生成一張人臉圖片的時候，不僅可以做到比較漂亮，而且它也是知道自己生成的時候哪部分是大尺度信息，哪部分是細節信息。就像一個畫家在作畫的時候，會自然地先去勾勒出他想畫的內容的輪廓，然后不斷地往里面完善細節，并且當我們想對某些細節做修改的時候可以很自然地去修改。而不是先畫左上角，完成了再畫左下角。

秉承重整化群流這個技術的核心思想，我們設計了更為復雜的神經網絡（RG-Flow）來在人臉圖片集（CelebA）上進行訓練。在訓練完成后我們可以看到（圖18a）機器會從大尺度先勾畫人臉的形狀，然后不斷添加細節信息，最終完成人臉的創作。為了更好地探究和理解機器是如何進行人臉生成的，我們借用視覺神經學和卷積神經網絡中感知域的概念，定義了我們生成模型中“神經元”的感知域。簡單的理解就是這些神經元對哪些圖片區域更加感興趣。通過我們的研究發現，其中很多神經元是不大活躍的，而其中活躍的神經元中可以看出非常有趣的事情。首先，越深層的神經元的感知域越大，越淺層的神經元的感知域越小。這是由我們重整化群想達到區分局域和全局信號的效果來保證的。而且這個和真正生物中的視覺中感知域的分布也是一致的。在生物視覺前段的視網膜神經細胞感知域大多是簡單的圓圈或者點，而后期的視覺皮層中視覺神經的細胞的感知域會變得更加復雜，來檢測看到視覺信號的一些圖案（pattern）。如圖18b所示，我們展現了我們的人工智能神經元的感知域分布，越靠上的感知域對于越深層的“人工神經元”。并且我們可以看出，對于越深層的“神經”，它的感知域會出現越來越多的圖案，比如眉毛、眼睛等等。

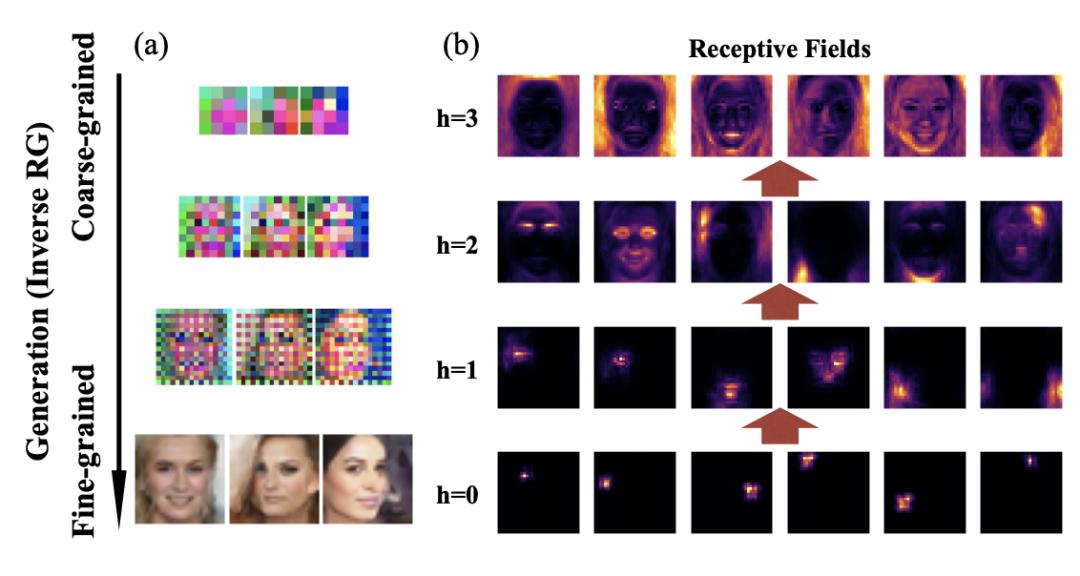
圖18

我們將會看到，這些對于特定區域反應強烈的“神經”，將會控制這個區域圖片的生成。比如：假設一個“神經”的感知域是眼睛，那它大概率會控制生成時候眼睛的大小。于是我們選取了不同層次上感知域較為強烈的“神經元”，來探索他們在圖像生成上究竟做了些什么。為了研究單個“神經”在圖像生成中的作用，分離出其他變量可能產生的影響，我們采取了在生成圖像時把所有的其他變量都控制不變，而只改變要研究的“神經”，讓它產生單獨的大小變化。通過這樣的系統研究，我們在不同層次上找到了一些具有可解釋性的“神經元”。

圖19

如圖19所示，在宏觀尺度上（或者是高層表示上），我們可以看到有“神經元”可以控制生成人像的性別（Gender），如果我們把它單獨從小調大，那么對應的人臉會逐漸減小女性特征，增強男性特征。再比如宏觀尺度上的情感（Emotion），我們如果改變這個“神經”的大小，對應的人臉會由中性狀態變為開心狀態。類似的在宏觀尺度上的因子（Factor）還有：光照（Light）、頭部旋轉（Azimuth）、發色（Hair）、膚色（Skin）。我們之前說到重整化群流（RG-Flow）最重要的是可以區分不同層級上的因子。所以在中等層級，我們也可以找到眼睛因子（Eye），它的改變對應于人臉眼睛的大小；發簾（Bang），它可以控制人像發簾的大小；眼眉（Eyebrow），它可以控制眼眉的粗細；衣領（Collar），它可以控制是否存在白色衣領。在小尺度上，我們也可以類似地找到控制單個眼眉、單個眼睛的因子。由于重整化群這個物理思想對于人工智能的指導，讓我們得以在訓練神經網絡的時候不僅可以生成我們想要的人像，并且它也不再是一個完全的黑盒，而是一個我們可以理解的生成人像的神經網絡。這些在不同層級上的控制因子可以讓我們對生成的圖片進行可控的調節。

圖20

類比于全息宇宙，我們可以想象這個神經網絡把二維的人臉圖片進行編碼并放到了三維的空間上，就如圖20a中樹狀網絡所示（為了簡單我們只畫了網絡的側面視圖，所以底下藍色的一維藍點可以認為是二維圖像）。圖片不同尺度的信息被排列在了樹狀網絡的縱深方向，這給了我們進行人像結合的一個新的維度。假設我們提供兩張人像圖片，如圖20a中的黑發女和金發女所示，現在我們可以把她們倆進行合成，我們想要保持黑發女人像的大尺度信息，比如她的發色、性別、表情，但是我們想要合成的人像具有金發女的細節信息，就是五官。那么我們可以把兩張圖片都在樹狀網絡的三維空間上進行編碼，然后在縱深的維度進行組合。結合深度將會決定生成的新的人臉有多少金發女的五官信息。類似的我們在圖20c中進行了更多的展示，比如上面一行7個人像作為高層級信息的源頭，左邊一列4個人像作為五官的信息源頭，我們可以合成出中間很多新的人像是他們的組合。

有了更多的理論支撐，基于重整化群的視覺生成模型也給了我們更多理論可控的分析。比如當我們的人像圖片產生局部的缺失需要復原的時候，我們的算法理論上可以在更短的時間（O(Log N)的復雜度）對圖片進行修復。如圖21所示，第一行為人像原圖，而第二行我們用紅色的色塊來表示有損失的人像。第三行是我們的機器對缺失信息填補之后的結果。

圖21

相信在不久的將來，我們會看到更多人工智能與物理學，科學碰撞而產生的火花。最后，對于更多動態圖片的展示與開源代碼，我們都將提供在GitHub上：

https://hongyehu.github.io/RG-Flow/

致 謝

本文涉及到的所有工作由作者和其導師尤亦莊、中科院物理所王磊老師、李爍輝博士、吳典博士生、伯克利人工智能實驗室陳羽北博士、Bruno Olsausen教授合作完成。作者還十分感謝在修改文章時Max Welling教授提出的寶貴意見，和與Koji Hashimoto教授在全息對偶上的交流，與吳從軍教授在重整化群上的交流。同時也感謝集智和凱風基金會對我們的大力支持。

引用：

[1] Shuo-Hui Li, Lei Wang. Phys. Rev. Lett. 121, 260601

[2] Hong-Ye Hu, Shuo-Hui Li, Lei Wang, Yi-Zhuang You. Phys. Rev. Research 2, 023369

[3] Hong-Ye Hu, Dian Wu, Yi-Zhuang You, Bruno Olsausen, Yubei Chen. ArXiv:2010.00029

課程推薦：

本視頻是作者對相關研究的講解

課程地址：

https://campus.swarma.org/course/2318/study

復雜科學最新論文

集智斑圖頂刊論文速遞欄目上線以來，持續收錄來自Nature、Science等頂刊的最新論文，追蹤復雜系統、網絡科學、計算社會科學等領域的前沿進展。現在正式推出訂閱功能，每周通過微信服務號「集智斑圖」推送論文信息。掃描下方二維碼即可一鍵訂閱：

原標題：《人臉和宇宙是啥關系？看物理學家怎樣用重整化群流模型重新理解視覺》

閱讀原文