陸晨博士  Dr. Chern Lu

香港大學SPACE中國商業學院 客席副教授

前海產業智庫首席國際金融學家

前平安磐海資本首席風險官

前華爾街著名投行副總裁 (Merrill Lynch、 Bear Stearns) 

美國紐約大學博士 

香港大學SPACE學院杰出教師2018/19

序言

在中國，高考是每一年中的一件至關重要的大事，是成千上萬的寒窗苦讀的學生們邁向自己所憧憬的人生旅程的第一道關口險隘。

今年，各地嚴峻的疫情形勢給 2022 年的高考增添了很多的不確定性，但隨著高考時間的臨近，各地疫情逐漸平復，讓家長們感到了一絲絲的欣慰。天氣也是出奇地給力，大概從我對高考有印象記憶開始，還沒有過這般恰似秋天的涼爽高考天！

高考的第一天下午就是考數學，隨著考試結束的鈴聲響起，考生們神情沮喪地走出考場，家長和老師們迫不及待地上前詢問數學考試的戰況如何，學生都不約而同地大吐苦水怨聲載道，吐槽數學考題真是太難了！線上的視頻中還有重點中學的學生難過得掉下了眼淚，可見今年數學考題殺傷力之大，波及四方。

解析人生真諦的貝葉斯推理

托馬斯·貝葉斯（Thomas Bayes，1702-1761），18世紀英國神學家、數學家、數理統計學家和哲學家，概率論理論創始人，貝葉斯統計的創立者，“歸納地”運用數學概率，“從特殊推論一般、從樣本推論全體”的第一人。

 P(A|B) = P(A)P(B|A) / P(B)

在上面著名的貝葉斯公式中，P(A)和P(B)都是先驗概率，而A有可能是誘發B的一個原因和條件。在觀察到事件B發生后對于事件A發生概率的預測是基于原來事件A發生的原始概率預測的一個修正和調整。而這個調整比例P(B|A) / P(B) 被稱為似然比。

在今年高考數學考卷中赫然發現一道貝葉斯推理計算題：

一個醫療隊研究某地的一種地方疾病與當地居民的衛生習慣（衛生習慣分為良好和不夠良好兩種）的關系，在患該疾病的病例中隨機調查了100例（稱為病例組），同時在未患有該疾病的人群中隨機調查了100人（成為對照組），得到了以下數據：

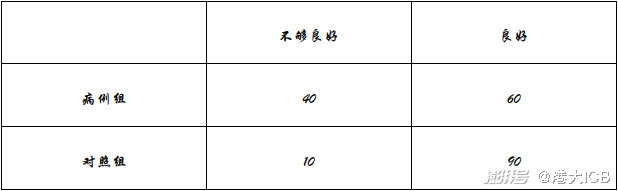
從該地的人群中人選一人，A事件表示“選到的人衛生習慣不夠良好”，B 事件表示“選到的人患有該疾病”。A事件表示 “選到的人衛生習慣良好” ，B事件表示 “選到的人未患有該疾病” 。P(B|A)/P(B|A)與P(B|A)/ P(B|A)的比值是衛生習慣不夠良好對于患該疾病風險程度的一項度量指標，記為R。

 R = P(A|B)/ P(A|B) * P(A|B)/ P(A|B) 

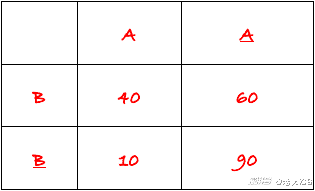
從上面題目所給的數據可以計算出來：

P(A|B)=40/100=0.4;

P(A|B)=10/100=0.1;

p(A|B)=60/100=0.6;

P(A|B)=90/100= 0.9;

R=0.4/0.6*0.9/0.1=6

這道題目很好地揭示了生活中一個非常重要的事實：兩個觀察到的現象，人們最為關心的就是因果關系，誰是誰的因，誰是誰的果。但是，統計學只能回答相關性而不能回答因果關系。在上面這道高考數學題目中，醫學工作者最感興趣的就是是否不良的生活習慣導致當地人染上這種疾病，第一層思維方式用概率語言來表示就是P(B|A)= P(A|B) * P(B)/P(A)。這就要求人們對于兩個先驗概率P(B)和P(A)有很好的估計，這兩個先驗概率的度量都需要大量的樣本調查，不僅工作量很繁重，同時統計誤差也會非常大。那么就直接導致這樣測算的結果 P(B|A)失真嚴重，所得到的結論也不能被完全相信。

基于以上的原因，直接回答P(B|A)不是一個好的方法。那么退而求其次，第二層的解決方案就在于通過對比具有良好習慣和不具有良好習慣的人群對于這種疾病患病率的影響。注意盡管在第一種方法中，計算的概率P(B|A)本身是一個條件概率，但是，從回答本問題的角度，這個概率是直接的方式。而第二種方法就是以比例 R 的形式出現，R 所度量的就是不良習慣對于患病和非患病人數的比例，再被良好習慣對于患病和非患病人數比例來正規化 Normalize，R是一個被兩次正規化的度量，這里最大的優點就是把誤差和噪音清除，我們不用再關心先驗概率P(B)和P(A)的嚴謹準確性。 

談到比例法的清除噪音揭示本質的特點，我給大家提供另外一個我在北大深圳研究院授課時引用的一個有趣例子來詮釋： 

假若有兩輛汽車，都有安全氣囊，一個防死亡率有效性是90%，另一個的有效性是70%，請問這兩輛車的安全性是“差不多”嗎？ 

在課堂上，大部分學生第一次看到這個問題，不明就里，覺得兩種安全氣囊的安全防護差不多，一個是90%，一個是70%，伯仲之間。但是，為了看清這個問題的真相，每個人最關心的是氣囊沒有防住風險，導致死亡的比例。從這個角度上講：第一種氣囊的死亡率是10%，第二種氣囊的死亡率是30%，第二種氣囊的死亡率是第一種氣囊的30%/10%=3倍。孰好孰壞，一目了然。

回到前面討論的主題，大家可以發現貝葉斯推理的本質就是利用一種可以在生活實踐中能清楚觀測到的事實和數據來合理地推算某些在實際中很難或者根本不可能觀察到的事實，這里面有很多是人們所向往的因果猜測！ 

在上面高考數學題中，P(A|B)是可以直接觀測到的統計數據，而相反，P(B|A)是無法直接觀察到的。因果關系的度量指標R最終是通過貝葉斯公式的神奇轉換，里面的參數都被可以直接觀察到的統計數據所替代，這就是數學之美數學的偉大。它能幫助人類順利完成了因果關系推導的不可能之任務。

金毛跑到哪去了？

我去年在疫情隔離期間無意中看到了一位同樣以概率思維為主線的教育工作者老喻的文章，開始關注他的動向。在最近的一篇文章中，老喻提出了一個非常耐人尋味的有趣問題，也是他在加拿大家里的真實經歷。我就用這個生動的例子來進一步說明偉大的貝葉斯推理在日常生活中如何提升人的深層認知能力，指導人們做出正確（有時候是艱難）的抉擇。 

假設一戶人家，男主人外出，突然接到家里的電話說是家里的愛犬金毛找不到了，男主人在安慰了家中的妻子和孩子之后，冷靜地根據歷史大數據做了如下的基本假設：金毛有

90%的概率在后院 

7%的概率跑出后院到了森林 

3%的概率被人偷走

男主人告訴家人在家里和后院仔細尋找，家人在后院找了一圈，沒有找到金毛，又再次焦急地打電話告訴男主人，問下一步如何尋找？假設在后院找過金毛但沒找到的概率是 10%，假設事件 A代表金毛還在后院，事件 B 代表在后院找了金毛，但沒有找到。 

那么，P(A)= 90%；P(A) = 10%。

利用貝葉斯推理的語言，這些都是通過歷史大數據總結的先驗概率。

根據已知條件，金毛還在后院，但沒有找到的概率很小，只有10%，用概率來表示就是P(B|A)=10%, 現在真正挑戰的是要計算出逆概率P(A|B)的大小，而P(A|B)所代表正是，已經在后院找過了沒有找到金毛，問在這種條件下，金毛還在后院的概率可能性。

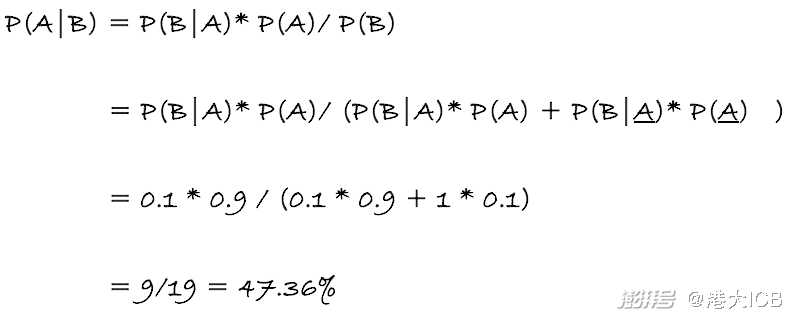
注意，在上面的計算中，P(B|A)=100%，是因為事件A代表金毛不在后院，那么肯定是找不到它的！ 

基于上面的計算，大家可以看到，即使第一次在后院尋找金毛，沒有找到，它還在后院的概率竟然還有近乎一半的概率可能性，遠遠大于另外兩種選擇7%和3%的概率！ 

根據老喻的親述，他就是經過上面的考量，再次打電話通知家人再到后院仔細找一次。家人們非常仔細把整個后院進行了地毯式搜索，四處大聲呼喚金毛的名字，突然聽到了悉悉索索的聲音，在后院Deck地毯下的一個隱藏的洞里發現了渾身是土驚慌失措的金毛，大家喜出望外地把它從洞中救了出來，貝葉斯推理救了金毛一命！ 

這個例子像極了發生在1968年的美國海軍天蝎號核潛艇在大西洋亞速海海域失蹤事件，潛艇和艇上的99名海軍官兵全部杳無音信……事后調查殘骸發現，罪魁禍首竟是潛艇自己發射的魚雷擊中了自己，多么不可思議！

美國海軍在茫茫的大西洋中苦苦搜尋了幾個月，一無所獲，只能求助于美國海軍的首席科學家John Craven，John不緊不慢地拿出一張標注著不同顏色的海洋地圖：

他又在白板上寫出來兩個數學公式：

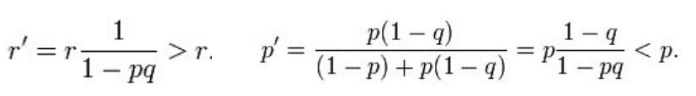
John把核潛艇沉沒的區域劃分成很多同樣大小的正方形，圖中每個格子所在的海域是考慮到魚雷沖擊波，水流等因素后潛艇殘骸可能散落的區域，p和q分別代表殘骸散落到某個格子的概率以及在該格子內能夠被找出來的概率，不一定核潛艇在某個格子就一定能被找出來，這和海域深度有關系。 

假設核潛艇在這個格子里的先驗概率為p= P(A)，潛艇在這個格子里，搜尋后發現潛艇的概率為q=P(B|A)，則類似于上面尋找金毛的問題，搜尋后沒有發現潛艇，但潛艇還是在該格子里的后驗概率，利用貝葉斯公式是：

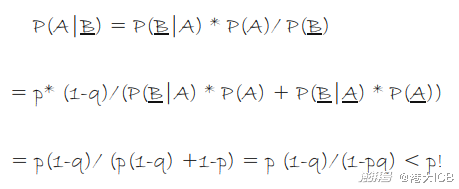
相反，對于另外的格子里找到核潛艇的概率，在得知在當前的格子中沒有發現潛艇的事實更新下，有以下的變化和調整：

也就是說每次搜尋完一個格子后，潛艇殘骸在這個格子里的概率p'就比之前p下降了；而同時，殘骸在其它格子的概率就會上升。所以，完成一次搜尋，全部區域都會重新洗牌，每次都會生成一個概率最大的格子，搜尋幾次后某個格子的概率就會特別大，美軍每次都駛向那個貝葉斯概率最大的方格，就真的很快找到沉沒的核潛艇。 

概率論中古老的貝葉斯推理竟然在 20 世紀幫助人類完成了一個幾乎是不可能的任務，再建新功。

貝葉斯推理在企業管理規劃中的應用

貝葉斯推理不僅在日常的工作生活中為我們做出正確的決定提供了一個嚴謹的思維框架，同樣的，它也在企業管理和規劃中大顯身手。隨著企業數字化的推廣，數字化技術不僅改變了下層的業務運營模式，更重要的是啟迪企業家運用更加科學的數字化思維來為企業未來的發展做決策，情景分析壓力測試等方法都被引入到了董事會的戰略分析中。

一種經典的場景就是企業面臨一個未來業務的決策，在做戰略分析研判的時候，董事會會引入未來不同的經濟場景，計算核查該項業務在不同場景下的得失和損益。

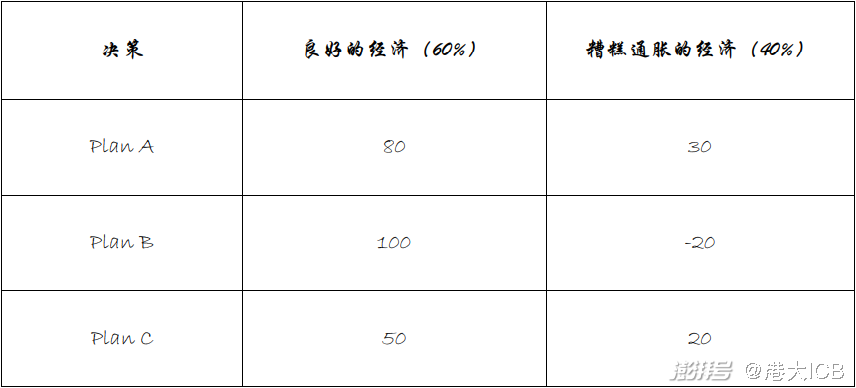
三種計劃的預期值計算出來是：

E(Plan A)=0.6*80+0.4*30=60（最佳） 

E(Plan B)=0.6*100+0.4*(-20)=52 

E(Plan C)=0.6*50+0.4*20=38 

這里的經濟好壞的概率都是先驗概率，總結歷史上的大數據得出的結論。但是，沒有人能未卜先知，知道未來的經濟狀況的好壞，為數不多的信息來源就是求助于經濟學家的報告和預測。假設，利用歷史大數據統計得出結論：在經濟狀況好的的時候，經濟學家有80%的概率得出正確的預判，有20%的概率做出錯誤的判斷。在經濟狀況不好的時候，有90%的概率預判正確，有10%的概率過于樂觀得出錯誤的結論。把這些條件寫成條件概率，就得到了下表：

假設經濟學家發布了正向的經濟報告，那么 

P(好經濟|正向報告)

=P(正向報告|好經濟)* P(好經濟)/P(正向報告) 

= P(正向報告|好經濟)* P(好經濟)/(P(正向報告|好經濟)*P(好經濟)+P(正向報告|不好經濟 )*P(不好經濟)） 

=0.8*0.6/(0.8*0.6+0.1*0.4)=12/13=92.3%

同樣的，P(不好經濟|正向報告) 

=P(正向報告|不好經濟)*P(不好經濟)/P(正向報告) 

=P(正向報告|不好經濟)*P(不好經濟)/(P(正向報告|好經濟)* P(好經濟)+P(正向報告|不好經濟)*P(不好經濟))

=0.1*0.4/(0.8*0.6+0.1*0.4)=1/13=1-92.3% = 7.7%

在更新的概率下，重新計算三種不同方案的預期值： 

E(Plan A)=0.923*80+0.077*30=76.15 

E(Plan B)=0.923*100+0.077*(-20)=90.76 （最佳） 

E(Plan C)=0.923*50+0.077*20=47.69 

概率思維是一種世界觀，統計思維是一種認識世界的方法論。有用的貝葉斯推理，人人都值得擁有。

（文章版權歸作者所有）